座標の回転
座標の回転は行列で表現できる。
座標変換の中でも、座標の回転はよく使われます。 座標の回転について簡単にまとめました。
2次元の場合(レベル1)
2次元のベクトルについて、座標を回転させる前のベクトル\(\bs{x}\)と 回転後のベクトル\(\bs{x}'\) の関係は \begin{equation} \label{rotate} \left (\begin{array}{c} x' \\ y' \end{array} \right) = \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta& \cos \theta \end{pmatrix} \left (\begin{array}{c} x \\ y \end{array} \right) \end{equation} でかける。(ただし、座標軸を負の方向に\(\theta\)だけ回した場合。)
二次元の回転です。 ちなみに、回転前と後のベクトルを関係づける以下の行列\(R(\theta)\) \begin{equation} \label{rotatemat} R(\theta)= \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta& \cos \theta \end{pmatrix} \end{equation} を回転行列といいます。(回転行列について詳しくは→回転行列)
証明
ここでは(\ref{rotate})式を証明します。極座標表示を使うと楽に示せます。 (ベクトルの極座標表示についてはこちらから)
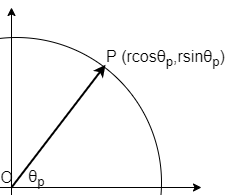
まず、回転前のベクトルの成分表示を、極座標をつかって図1のように \begin{equation} \left (\begin{array}{c} x \\ y \end{array} \right) = \left (\begin{array}{c} r \cos \theta_{p} \\ r \sin \theta_{p} \end{array} \right) \end{equation} とかいておく。今、座標軸を図2のように\(\theta\)だけ回転させた場合を考える。
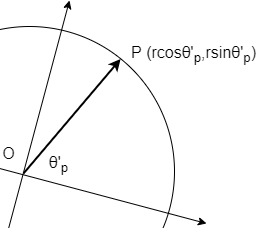
すると、回転後の成分表示は \begin{equation} \left (\begin{array}{c} x' \\ y' \end{array} \right) = \left (\begin{array}{c} r \cos \theta'_{p} \\ r \sin \theta'_{p} \end{array} \right) \end{equation} ここに、\(\theta'_{p}=\theta_{p}+\theta\)である。(座標軸を負の方向へ\(\theta\)だけ回したということ 。または、\(\overrightarrow{OP}\)を正の方向へ\(\theta\)回したとも今は思ってもよい。)
さて、加法定理により、 \begin{eqnarray} \cos \theta'_{p}=\cos \theta_{p} \cos \theta-\sin \theta_{p} \sin \theta \\ \sin \theta'_{p}=\sin \theta_{p} \cos \theta+ \cos \theta_{p} \sin \theta \end{eqnarray} であるから、行列を使ってかくと、 \begin{equation} \label{poler} \left (\begin{array}{c} r \cos \theta'_{p} \\ r \sin \theta'_{p} \end{array} \right) = \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta& \cos \theta \end{pmatrix} \left (\begin{array}{c} r \cos \theta_{p} \\ r \sin \theta_{p} \end{array} \right) \end{equation} であり、以上より(\ref{rotate})式が示せた。
座標軸を負の向きに回す代わりに、\(\overrightarrow{OP}\)を正の方向へ\(\theta\)回した 場合も同じ結果 \begin{equation} \left (\begin{array}{c} x' \\ y' \end{array} \right) = \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta& \cos \theta \end{pmatrix} \left (\begin{array}{c} x \\ y \end{array} \right) \tag{\ref{rotate}} \end{equation} になります。
また、逆回転の場合は\(\theta\)を\(-\theta\)に変えて計算すればよく、結果は \begin{equation} \label{reverse} \left (\begin{array}{c} x' \\ y' \end{array} \right) = \begin{pmatrix} \cos \theta & \sin \theta \\ -\sin \theta& \cos \theta \end{pmatrix} \left (\begin{array}{c} x \\ y \end{array} \right) \end{equation} になります。簡単ですね。
また、(\ref{poler})式に おいて、\(\theta=-\theta_{p}\)の場合を計算すると \(\theta'_{p}=0\)より、 \begin{equation} \left (\begin{array}{c} r \\ 0 \end{array} \right) = \begin{pmatrix} \cos \theta_{p} & \sin \theta_{p} \\ -\sin \theta_{p} & \cos \theta_{p} \end{pmatrix} \left (\begin{array}{c} x \\ y \end{array} \right) \end{equation} を得ます。左辺は極座標基底での成分表示になっています。 このことからも、極座標の基底は、普通のデカルト座標を回転させたもの に対応していることが分かります。
3次元の場合(レベル2)
3次元のベクトルについて、座標の回転のさせかたは、 \(x\)軸を回転の軸としたもの、\(y\)軸を回転の軸としたもの、 そして\(z\)軸を回転の軸としたもの、以上の3通りある。
3次元の回転は2次元の場合と異なり、3通りありますが、それぞれの軸回りの 回転について、行列で表現が可能です。
回転前のベクトルを\(\bs{x}\)、回転後のベクトルを\(\bs{x}'\)と すると、 \begin{equation} \label{rotate3} \bs{x}'=R_{x_{i}}(\theta_{x_{i}}) \bs{x} \end{equation} が成り立つ。ただし、\(x_{i} \ (i=1,2,3)\)は 回転の軸を表し、\(R_{x_{i}}\)はそれぞれの軸の対応する 回転行列を表す。
3次元の回転行列の一覧は以下の通りです。(\(\theta_{x_{i}}\)は、 \(x_{i}\)軸回りに回転させた角度)
\begin{equation} \label{rotatematx} R_{x}(\theta_{x})= \begin{pmatrix} 1 & 0 & 0 \\ 0& \cos \theta_{x} & -\sin \theta_{x} \\ 0 & \sin \theta_{x} & \cos \theta_{x} \end{pmatrix} \end{equation} \begin{equation} \label{rotatematy} R_{y}(\theta_{y})= \begin{pmatrix} \cos \theta_{y} & 0 & \sin \theta_{y} \\ 0& 1 & 0 \\ -\sin \theta_{y} & 0 & \cos \theta_{y} \end{pmatrix} \end{equation} \begin{equation} \label{rotatematz} R_{z}(\theta_{z})= \begin{pmatrix} \cos \theta_{z} & -\sin \theta_{z} & 0 \\ \sin \theta_{z} & \cos \theta_{z}& 0 \\ 0 & 0 & 1 \end{pmatrix} \end{equation}今回は(\ref{rotate3})式が成り立つことを、 2次元の場合と同じように成分を計算する方法と、回転軸を置き換える方法の2通りで証明します。
証明その1
ここでは、\(x\)軸回りの回転が(\ref{rotatematx})式で書けることを示そうと 思います。他の軸についても全く同様の計算で示すことができます。
方針としては、2次元の時と同じように\(\bs{x}\)を極座標表示し、加法定理を使います。この際、 通常の極座標のような、\(z\)軸を特別視したものだと\(x\)軸回りの回転角度\(\theta_{x}\)が出てこない ので、\(x\)軸を特別視する極座標を使います。
まず、回転前のベクトルの成分表示を、極座標を使い \begin{equation} \left (\begin{array}{c} x \\ y \\ z \end{array} \right) = \left (\begin{array}{c} r \cos \theta_{c} \\ r \sin \theta_{c} \cos \theta_{x_{0}} \\ r \sin \theta_{c} \sin \theta_{x_{0}} \end{array} \right) \end{equation} とかく。ここで、\(\theta_{c}\)は\(x\)軸とのなす角、\(\theta_{x_{0}}\)は \(x\)軸回りの角度。そして回転後成分表示も同様に \begin{equation} \left (\begin{array}{c} x \\ y \\ z \end{array} \right) = \left (\begin{array}{c} r \cos \theta_{c} \\ r \sin \theta_{c} \cos \theta'_{x_{0}} \\ r \sin \theta_{c} \sin \theta'_{x_{0}'} \end{array} \right) \end{equation} と表せる。(回転の前後で、\(x\)軸とのなす角度\(\theta_{c}\)が変わらないことに注意。)
さて、回転角度を\(\theta_{x}\)とすると、 \(\theta'_{x_{0}}=\theta_{x_{0}}+\theta_{x}\)なので、加法定理が使える。 あとはその結果を行列でかくと \begin{equation} \left (\begin{array}{c} r \cos \theta_{c} \\ r \sin \theta_{c} \cos \theta'_{x_{0}} \\ r \sin \theta_{c} \sin \theta'_{x_{0}} \end{array} \right) = \begin{pmatrix} 1 & 0 & 0 \\ 0& \cos \theta_{x} & -\sin \theta_{x} \\ 0 & \sin \theta_{x} & \cos \theta_{x} \end{pmatrix} \left (\begin{array}{c} r \cos \theta_{c} \\ r \sin \theta_{c} \cos \theta_{x_{0}} \\ r \sin \theta_{c} \sin \theta_{x_{0}} \end{array} \right) \end{equation} となるため、以上により \(x\)軸回りの回転が(\ref{rotatematx})式で書けることを示せた。他の成分も同様にして 示せる。
もう一つの証明は、軸のいれかえを使う方法です。
証明その2
方針として、2次元との類似性から\(z\)軸回りの回転について (\ref{rotatematz})式を先に示し、 あとの二つを軸の入れ替えによって導きます。この入れ替えは、 順番が重要であり、常に座標が右手系になるように注意する必要があります。
まず、\(z\)軸回りの回転が(\ref{rotatematz})式で書けることを示す。 \(z\)軸回りの回転の場合、これは\(xy\)平面上の回転であるため、 (\(z\)成分は不変であるまた、2次元の回転もまた、\(xy\)平面上での回転であるため \begin{equation} \label{rotatez} \left (\begin{array}{c} x' \\ y' \\ z' \end{array} \right) = \begin{pmatrix} \cos \theta_{z} & -\sin \theta_{z} & 0 \\ \sin \theta_{z} & \cos \theta_{z}& 0 \\ 0 & 0 & 1 \end{pmatrix} \left (\begin{array}{c} x \\ y \\ z \end{array} \right) \end{equation} がいえる。よって(\ref{rotatematz})式がいえた。
さて、(\ref{rotatez})式について行列を使わずに書き下すと以下のようになる。 \begin{eqnarray} x'&=& \cos \theta_{z} x-\sin \theta_{z} y + 0 \cdot z \\ y'&=& \sin \theta_{z} x+ \cos \theta_{z} y + 0 \cdot z \\ z'&=& 0 \cdot x +0 \cdot y +z \end{eqnarray} ここで、次のように軸の名前を入れ替える \(x \to y, y \to z, z \to x\)。すると、上の3つの式は \begin{eqnarray} y'&=& \cos \theta_{x} y-\sin \theta_{x} z + 0 \cdot x \\ z'&=& \sin \theta_{x} y+ \cos \theta_{x} z + 0 \cdot x \\ x'&=& 0 \cdot y +0 \cdot z +x \end{eqnarray} のように変化する。(軸の入れ替えにより、 \(\theta_{z}\)も\(\theta_{x}\)に置き換わることに注意) これを行列で書き直すと \begin{equation} \left (\begin{array}{c} x' \\ y' \\ z' \end{array} \right) = \begin{pmatrix} 1 & 0 & 0 \\ 0& \cos \theta_{x} & -\sin \theta_{x} \\ 0 & \sin \theta_{x} & \cos \theta_{x} \end{pmatrix} \left (\begin{array}{c} x \\ y \\ z \end{array} \right) \end{equation} を得る。これは(\ref{rotatematx})式にほかならない。 さらに軸の名前を入れ替えて、\(x \to y, y \to z, z \to x\)とすると (\ref{rotatematy})式も得られる。
基底の回転(レベル2)
基底ベクトルの回転は、ベクトルの成分表示と同じように書ける。
座標軸を負の方向に\(\theta\)回した時、ベクトルの成分は上でやったように変化しますが、基底ベクトルも変化します。 ここでは、その一例として、2次元の場合、回転の前後で基底ベクトルが \begin{equation} \label{basis} \left (\begin{array}{c} \bs{e}_{x'} \\ \bs{e}_{y'} \end{array} \right) = \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta& \cos \theta \end{pmatrix} \left (\begin{array}{c} \bs{e}_{x} \\ \bs{e}_{y} \end{array} \right) \end{equation} のように変化することを示します。
ベクトルの成分表示が、自身の正の回転\(\theta\)により、 \begin{equation} \left (\begin{array}{c} x' \\ y' \end{array} \right) = \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta& \cos \theta \end{pmatrix} \left (\begin{array}{c} x \\ y \end{array} \right) \tag{\ref{rotate}} \end{equation} になることを鑑みると、成分表示と基底ベクトルは互いに逆回転で変化することが分かります。
証明
(\ref{basis})式の証明は、図を使うと分かりやすいです。
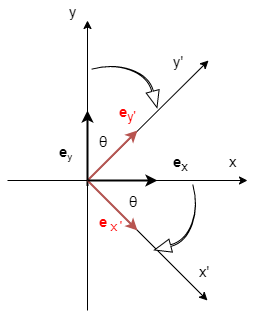
この図から、 \begin{eqnarray} \bs{e}_{x'}= \cos \theta \bs{e}_{x} -\sin \theta \bs{e}_{y} \\ \bs{e}_{y'}= \cos \theta \bs{e}_{x} + \sin \theta \bs{e}_{y} \end{eqnarray} と分かります。これを行列表示することで、(\ref{basis})式を得ます。