ベクトルの極座標表示
デカルト座標の変数\((x,y)\)の代わりに、 極座標の変数\((r,\theta)\)でベクトルを表示することができる。
ベクトルは座標によって変化しませんが、成分表示 をした場合、見た目だけ変わります。
混乱しやすいところなので、言葉を慎重に選んで解説していきます。 ここでは、ベクトルを\(r,\theta\)を使って成分表示することを 極座標表示と呼ぶことにします。
極座標表示(レベル1)
位置ベクトル \begin{equation} \bs{r}= \left (\begin{array}{c} x \\ y \end{array} \right) \end{equation} は\((r,\theta)\)を使って、 \begin{equation} \label{polar} \bs{r}= \left (\begin{array}{c} r \cos \theta \\ r \sin \theta \end{array} \right) \end{equation} と極座標表示することが可能。
基本的な関係式です。これは極座標へ座標変換するときの公式 \begin{equation} \left (\begin{array}{c} x \\ y \end{array} \right) = \left (\begin{array}{c} r \cos \theta \\ r \sin \theta \end{array} \right) \end{equation} を使うだけですぐに導けます。
注意点として、(\ref{polar})式の変数(成分)は極座標で表示されていますが、 基底はデカルト座標のままです。成分表示のままだと分かりにくいですが、 基底は変えずに、ただ変数のみ変換したものが(\ref{polar})式ということです。 (成分表示と基底表示の違いについてはこちらの記事を参照。)
これは基底表示との対応でかけば \begin{eqnarray} \left (\begin{array}{c} x \\ y \end{array} \right) & \longleftrightarrow & x \bs{e}_{x}+y \bs{e}_{y} \\ \left (\begin{array}{c} r \cos \theta \\ r \sin \theta \end{array} \right) & \longleftrightarrow & r \cos \theta \bs{e}_{x}+r \sin \theta \bs{e}_{y} \end{eqnarray} になっているので、基底はデカルト座標のままということが見やすいですね。
極座標基底による成分表示(レベル1)
デカルト座標の基底\(\bs{e}_{x},\bs{e}_{y}\) の代わりに、極座標の基底\(\bs{e}_{r},\bs{e}_{\theta}\)を使って ベクトルを成分表示することができる。
極座標の基底を定義すれば、どんなベクトルもその基底を使って成分表示する ことが可能です。 (極座標の基底について詳しくは下のギモン参照。)
まずは具体例を挙げてみます。
具体例
位置ベクトル\(\bs{r}\)は極座標の基底\(\bs{e}_{r}\)を 使って、 \begin{equation} \label{basis} \bs{r}=r \bs{e}_{r} \end{equation} と展開できる。ゆえに、極座標基底で成分表示すると \begin{equation} \label{rcomponent} \bs{r}= \left (\begin{array}{c} r \\ 0 \end{array} \right) \end{equation} である。
基底表示との対応でかくと \begin{equation} \left (\begin{array}{c} r \\ 0 \end{array} \right) \longleftrightarrow r \bs{e}_{r}+0 \bs{e}_{\theta} \end{equation} である。
補足しておくと、極座標の成分表示 (\ref{rcomponent})式はほとんど使いません。 基底展開した表式(\ref{basis})は公式の導出にたまに使います。 このため、ベクトルの極座標表示といえばもっぱら (\ref{polar})式のことを指します。
また、成分表示した結果(\ref{rcomponent})式が、極座標の座標\((r,\theta\)) とは異なっていることにも注意です。 (デカルト座標の場合は、成分表示と座標は同じく\((x,y)\) になっていましたね)
ほかには、等速円運動の速度ベクトル\(\bs{v}\)は \begin{equation} \bs{v}=r \dot{\theta} \bs{e}_{\theta} \end{equation} と展開できるので、極座標基底で成分表示すると \begin{equation} \bs{v}= \left (\begin{array}{c} 0 \\ r \dot{\theta} \end{array} \right) \end{equation} のようになります。
極座標基底(レベル1)
原点から物体への方向を\(r\)方向とした時、これに垂直な方向を \(\theta\)方向と定める。それぞれの方向に対応する 単位ベクトルを\(\bs{e}_{r},\bs{e}_{\theta}\)と表記し、 これらを極座標の基底ベクトルと呼ぶ。
極座標の基底ベクトルの定義です。\(\theta\)軸は角度\(\theta\)が増える向き を正にとります。
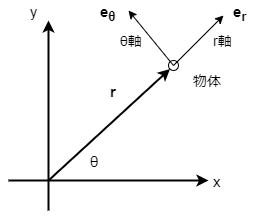
上の具体例でも触れましたが、 極座標の座標が\((r,\theta)\)の時、対応する座標ベクトルを極座標基底で成分表示すると \((r,0)\)になります。 両者が同じ表記になったデカルト座標の場合とは異なるので 注意してください。
また、図の通り、\(r\)軸は\(x\)軸を角度\(\theta\)だけ回転させたもの、 同様に\(\theta\)軸は\(y\)軸を角度\(\theta\)だけ回転させたものになっています。 (図では分けて描写したが、両者の原点は本来同一)
基底\(\bs{e}_{r},\bs{e}_{\theta}\) はそれぞれ極座標の変数\((r,\theta)\)を用いて \begin{equation} \label{rbasis} \bs{e}_{r}= \left (\begin{array}{c} \cos \theta \\ \sin \theta \end{array} \right) \end{equation} \begin{equation} \label{thetabasis} \bs{e}_{\theta}= \left (\begin{array}{c} -\sin \theta \\ \cos \theta \end{array} \right) \end{equation} と表せる。
極座標の基底\(\bs{e}_{r},\bs{e}_{\theta}\)も当然 (\ref{polar})式のように極座標表示できます。 (\ref{polar})式と同様の注意として(\ref{rbasis})、(\ref{thetabasis})式 の右辺はデカルト座標の基底による成分表示です。 基底をあらわにかくと \begin{eqnarray} \bs{e}_{r}&=& \cos \theta \bs{e}_{x}+ \sin \theta \bs{e}_{y} \\ \bs{e}_{\theta}&=& -\sin \theta \bs{e}_{x} +\cos \theta \bs{e}_{y} \end{eqnarray} ということです。
導出
\begin{equation} \bs{e}_{r}=\frac{\bs{r}}{r} \end{equation} より、(\ref{polar})式を代入すれば (\ref{rbasis})式が求まる。
つづいて、図より、\(\bs{e}_{\theta}\)は \(\bs{e}_{r}\)を\(\frac{\pi}{2}\)だけ回転させたものである。 ゆえに、(\ref{rbasis})式の\(\theta\)を \(\theta+\frac{\pi}{2}\)に置き換えて計算すると \begin{equation} \left (\begin{array}{c} \cos (\theta+\frac{\pi}{2}) \\ \sin (\theta+\frac{\pi}{2}) \end{array} \right) = \left (\begin{array}{c} -\sin \theta \\ \cos \theta \end{array} \right) \end{equation} より\(\bs{e}_{\theta}\)の表式(\ref{thetabasis})の右辺に一致した。