自由落下その2(空気抵抗がある場合)
空気抵抗のある場合の自由落下は以下の運動方程式 \begin{equation} \label{downwardeq} m\frac{d^2 x(t)}{dt^2}=mg - \kappa \frac{dx(t)}{dt} \end{equation} に従う。(ただし、\(\kappa>0\)で、下向き正でとった)
空気抵抗のある場合には、減衰項と呼ばれる\(- \kappa \frac{dx(t)}{dt}\)が 加わります。
(\ref{downwardeq})式では\(x\)軸を図1のように物体が落ちる方向が正 (つまり下向き正) になるようにとっています。右辺が\(-mg\)ではなく、\(mg\)であるのはそのためです。
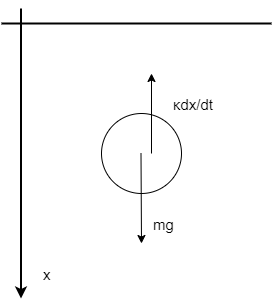
逆に、物体の落ちる方向を負、つまり上向き正で座標を取ると、運動方程式は \begin{equation} \label{upwardeq} m\frac{d^2 x(t)}{dt^2}=-mg - \kappa \frac{dx(t)}{dt} \end{equation} になります。詳しくは当該ギモン参照。
一般解(レベル1)
早速運動方程式を解いて解を求めていきましょう。このあたりから、少し技巧が必要になってきます。
以下の形の二階微分方程式 \begin{equation} f''(t)+a f'(t)+b=0 \end{equation} (ただし、\(a\)、\(b\)は定数)は\(g(t)=f'(t)\)と置きなおすことで 一階の微分方程式 \begin{equation} g'(t)+a g(t)+b=0 \end{equation} に帰着できる。
二階の微分方程式を急に解くのは難しいため、まずは一階の微分方程式にして問題を簡単にしましょう。 シンプルな発想ですが、今後、この変形は何度か見ることになります。
(\ref{downwardeq})式は\(v(t)=\frac{d x}{dt}(t)\)とおくことで、
\begin{equation}
\label{diffeq}
\frac{d v(t)}{dt}=g - h v(t)
\end{equation}
(ただし\(h=\frac{\kappa}{m}\)とおいた)
なる一階の微分方程式に帰着できます。
この形の微分方程式は一階非同次微分方程式と呼ばれます。
気になる人は→一階微分方程式(非同次)
以下の微分方程式 \begin{equation} \frac{d v(t)}{dt}=g - h v(t) \tag{\ref{diffeq}} \end{equation} (ただし\(g,h>0\))の一般解は \begin{equation} \label{gsolution} v(t)=C_{0} e^{-ht}+\frac{g}{h} \end{equation}
まだ一階なので、コツさえ掴めば簡単に積分できます。
導出
(\ref{diffeq})式について、両辺を\(g - h v(t)\)で割って積分を行う。 (左辺に\(v\)を集めるのが、この微分方程式の解き方の肝) \begin{eqnarray} \int \frac{1}{ g-hv(t) } dv=\int dt \end{eqnarray} 更に積分が楽になるように分母の\(v(t)\)の係数が1になるようにする。 (\(h\)がかかっていると、合成関数の積分を考えなければいけないので注意) すると、 \begin{eqnarray} \int \frac{1}{ v(t)-\frac{g}{h} } dv=-\int hdt \end{eqnarray} まで変形ができる。
あとは普通に積分を実行すれば、 \begin{equation} \log (v(t)-\frac{g}{h})=-ht+C \end{equation} ただし、\(C\)は積分定数。これにより \begin{equation} v(t)=\frac{g}{h}+e^{-ht+C} \end{equation} さらに指数関数の公式から \begin{equation} e^{-ht+C}=e^{-ht} e^{C} \end{equation} と書けるから、結局解は\(C_{0}=e^{C}\)と置きなおすと、 \begin{equation} v(t)=C_{0} e^{-ht}+\frac{g}{h} \tag{\ref{gsolution}} \end{equation} となって解が求まった。
以下の微分方程式 \begin{equation} \frac{d^2 x(t)}{dt^2}=g - h \frac{dx(t)}{dt} \end{equation} の一般解は \begin{equation} x(t)=-C_{0}\frac{1}{h} e^{-ht}+\frac{g}{h}t+C_{1} \end{equation} である。
(\ref{gsolution})式をさらに積分することで、運動方程式の解 \(x(t)\)が求まります。(上では\(h=\frac{\kappa}{m}\)とおいています。)
一般に、微分の階数分だけ、未知定数(\(C_{0}\)とか\(C_{1}\))が解に 現れることが知られています。
物理的意味(レベル1)
一般解が分かったところでその物理的意味について考察していきます。 特に速度について、以下の有名な事実が成り立ちます。
空気抵抗ありの自由落下について初期条件\(v(0)=v_{0}\)を与えた時、 速度は \begin{equation} v(t)= (v_{0}-\frac{mg}{\kappa})e^{-\frac{\kappa}{m}t}+\frac{mg}{\kappa} \end{equation} でかけるが、\(t \to \infty\)の極限を取ると、\(v_{0}\)の値によらず \begin{equation} v(t) \to \frac{mg}{\kappa} \end{equation} に収束する。この時の\(v(\infty)=\frac{mg}{\kappa} \)を終端速度と呼ぶ。
空から自由落下する雨粒は、ほぼ終端速度で落下しています。もし空気抵抗がなければ、拳銃に匹敵する 速度で落下するようです。また、終端速度が初期条件に依らないため、雲の中の様子によらず 雨は一様な速度で落下することが示唆されています。(質量には依存する)
座標軸が上向き正の場合(レベル1)
空気抵抗のある場合の自由落下は以下の運動方程式 \begin{equation} m\frac{d^2 x(t)}{dt^2}=-mg - \kappa \frac{dx(t)}{dt} \tag{\ref{upwardeq}} \end{equation} に従う。(ただし、\(\kappa>0\)で、上向き正でとった)
上では座標軸が下向き正で議論をすすめましたが、上向き正 でとった場合を考えます。対応する図は以下の通りです。
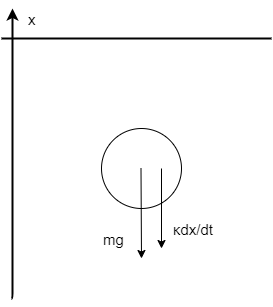
今回は速度が負(\(\frac{dx(t)}{dt}<0\))のため空気抵抗の向きが変なことになっています。 原因は減衰は必ず速度正の方向と逆向きに働くと約束しているためで、気持ち悪いですが方向はこれで合っています。 一応、(\ref{downwardeq})式から(\ref{upwardeq})式を導いておきます。
導出
\(x\)軸の正負を反転させる変換は\(x \to -x\)で表せる。(\ref{downwardeq})式 にこの変換を施すと、 \begin{equation} -m\frac{d^2 x(t)}{dt^2}=mg + \kappa \frac{dx(t)}{dt} \end{equation} になり、両辺に\(-1\)をかけることで、 \begin{equation} m\frac{d^2 x(t)}{dt^2}=-mg - \kappa \frac{dx(t)}{dt} \tag{\ref{upwardeq}} \end{equation} を得る。
(\ref{upwardeq})式も同様にして解を求めることができます。概略のみ示しておきます。
計算
\(v(t)=\frac{dx}{dt}\)と置くと、 \begin{equation} m\frac{d v(t)}{dt}=-mg - \kappa v(t) \end{equation} となり、あとは同じように計算すると、 \begin{eqnarray} & \ &\frac{m}{-mg - \kappa v(t)} dv=dt \\ & \ &\int \frac{1}{ v(t)+\frac{mg}{\kappa} } dv=-\int \frac{\kappa}{m}dt \end{eqnarray} これを実行して \begin{equation} v(t)=-\frac{mg}{\kappa}+\exp[-\frac{\kappa}{m}t+C] \end{equation} ただし\(C\)は積分定数となる。最後に\(C_{0}=e^{C}\)と置きなおすと、 \begin{equation} \label{gsolution2} v(t)=C_{0} e^{-\frac{\kappa}{m}t}-\frac{mg}{\kappa} \end{equation} となって解が求まった。さて、このようにして得られた\(v(t)\)をよく見てやると色々面白いことが分かります。
まず、この(\ref{gsolution2})式について、\(t \to \infty\)をとってやると \(v(t) \to -\frac{mg}{\kappa} \)となって終端速度の符号が下向き正の時と比べ反転していることが分かります。
また、正負を反転する変換\(v(t) \to -v(t)\)を考えてやると、 \begin{equation} v(t)=-C_{0} e^{-\frac{\kappa}{m}t}+\frac{mg}{\kappa} \end{equation} になりますが、\(-C_{0}\)はただの定数なのでこれを\(C_{0}\)と置きなおすと、確かに(\ref{gsolution})式に一致し、矛盾がないことが 確かめられました。