デルタ関数とその性質
今回のギモン(クリックすると当該セクションへ)
適当な関数\(f(x)\)に対し、 \begin{equation} \label{delta} \int_{-\infty}^{\infty} f(x) \delta(x-a)dx=f(a) \end{equation} を満たすような\(\delta(x)\)をデルタ関数と呼ぶ。
物理の様々な分野で顔を出すデルタ関数についてここでは簡単にまとめます。 ちなみに、デルタ「関数」という名前ですが、厳密では関数ではありません。数学的には超関数というくくりに入るようです。
ここでは主にデルタ関数の基本的な性質について解説します。 また、フーリエ変換(積分表示)について知りたい人は デルタ関数の有名表式へ。
定義の直感的な説明(レベル1)
\(\delta(x)\)は形式上以下のような関数と思える。 \begin{equation} \label{deltavalue} \delta(x)= \begin{cases} 0 & x \neq 0 \\ \infty & x=0 \\ \end{cases} \end{equation} つまり原点で発散し、原点以外では\(0\)になるような関数。
デルタ関数はディラックが物理へ持ち込んだとんでも関数です。引数が\(0\)になると発散し、 それ以外では\(0\)になります。図示すると図1のような見た目になります。
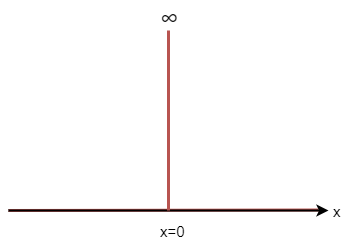
原点で一本縦にピークが立っているような見た目ですね。
さて、上では\(\delta(x)\)を考えていますが、例えば\(\delta(x-a)\)なら、
\begin{equation}
\delta(x-a)=
\begin{cases}
0 & x \neq a \\
\infty & x=a \\
\end{cases}
\end{equation}
のようになります。これは丁度、発散する位置が\(a\)だけ平行移動した形になっています。
また、定義式(\ref{delta})式と見比べると、\(\delta(x-a)\)が\(a\)以外で\(0\)なので、\(f(x)\)
のうち\(f(a)\)のみが抽出されているのだと理解できます。
ちなみにですが、(\ref{delta})式は適当な\(f(x)\)で成り立つ式なので 当然\(f(x-a)\)についても \begin{equation} \int_{-\infty}^{\infty} f(x-a) \delta(x-a)dx=f(a-a)=f(0) \end{equation} がいえます。ここで\(t=x-a\)と置くと \begin{equation} \int_{-\infty}^{\infty} f(t) \delta(t) dt=f(0) \end{equation} のように原点にピークを持つデルタ関数の表式に帰着できます。このため、デルタ関数の定義を以下のよう に書くこともあります。
適当な関数\(f(x)\)に対し、 \begin{equation} \label{delta2} \int_{-\infty}^{\infty} f(x) \delta(x)dx=f(0) \end{equation} を満たすような\(\delta(x)\)をデルタ関数と呼ぶ。
基本的な性質(レベル1~2)
\(\delta(x-a)\)は全区間で積分すると\(1\)。つまり \begin{equation} \label{normalization} \int_{-\infty}^{\infty} \delta(x-a)dx=1 \end{equation}
デルタ関数の定義(\ref{delta})式において、\(f(x)=1\)の場合を考えると明らかです。 図1のグラフを見ると原点で形式上発散していますが、積分するとこれは\(1\)になるということです。これはデルタ関数の持つ基本中の基本的な 性質ですね。
デルタ関数は(\ref{delta})式のように、積分の中で定義される関数である。 ゆえにデルタ関数についての等式は、暗に積分の中にあると約束する。
ここから、いくつかデルタ関数の満たす性質(等式)を説明しますが、デルタ関数は普通の関数とは 違って積分の中でしか定義されません。なのでそのことを念頭に置く必要があります。
例えば(\ref{delta})式と(\ref{normalization})式より、 \begin{eqnarray} \int_{-\infty}^{\infty} f(x) \delta(x-a)dx &=& f(a) \\ f(a) \int_{-\infty}^{\infty} \delta(x-a)dx \ &=& f(a) \end{eqnarray} なので、両者は等しく \begin{eqnarray} & & \int_{-\infty}^{\infty} f(x) \delta(x-a)dx \nonumber \\ \label{deltaeq} &=&\int_{-\infty}^{\infty} f(a) \delta (x-a)dx \end{eqnarray} が成り立ちますが、これを単に積分を略記して \begin{equation} \label{deltaeq2} f(x) \delta(x-a)=f(a) \delta (x-a) \end{equation} とすることが多々あります。しかし、デルタ関数は積分の中にあって始めて定義される関数なので、 本当の意味は(\ref{deltaeq})式ということを忘れないようにしましょう。
\(\delta(x)\)と適当な関数\(f(x)\)について以下が成り立つ \begin{equation} f(x) \delta(x-a)= f(a) \delta (x-a) \tag{\ref{deltaeq2}} \end{equation} 特に、\(f(x)=(x-a)\)の時、 \begin{equation} (x-a) \delta(x-a)= 0 \end{equation} である。これは両辺をそれぞれ積分すると確認できる。
デルタ関数には他にも有用な性質がいくつかあります。
\(\delta(x)\)は偶関数の性質を持つ。即ち \begin{equation} \delta(x)= \delta(-x) \end{equation} である。
図1のグラフ

ただし、上で述べた通り、この等式は積分の中に入って初めて意味を持つので注意してください。
この性質より、\(f(x)\)が奇関数の時、
\begin{equation}
\int_{-\infty}^{\infty} f(x) \delta(x)dx=0
\end{equation}
になります。典型的なのは、\(f(x)=x\)の場合などです。
証明についてはデルタ関数の公式(基本編)へ。
\(a\)を\(0\)ではない実数として、デルタ関数について以下が成り立つ。 \begin{equation} \label{atimesdelta} \delta(ax)= {1 \over |a|} \delta(x) \end{equation}
比較的よく使うデルタ関数の公式です。証明は デルタ関数の公式(基本編)を 参照してください。
デルタ関数は発散するか\(0\)しかないので、\({1 \over |a|}\)だけスケールが変わっても 無意味なように思えるかもしれません。このような係数がつく理由は「デルタ関数が積分して\(1\)になる」という性質のためです。 \begin{equation} \int_{-\infty}^{\infty} \delta(|a|x)d|a|x=1 \end{equation} 上記のように、積分要素が\(dx \to d(|a|x)=|a| dx\)だけ変わった時、その変化を打ち消すように \(\delta(x) \to \delta(|a|x)={1 \over |a|} \delta(x)\)だけ変化すれば、辻褄があって確かに\(1\)に なることが分かります。
デルタ関数は \begin{equation} \delta(x)= \begin{cases} 0 & x \neq 0 \\ \infty & x=0 \\ \end{cases} \tag{\ref{deltavalue}} \end{equation} のように、ピーク以外の値は\(0\)である。ゆえに、ピーク以外の積分範囲は 落としても計算に支障はない。例えば \begin{eqnarray} & & \int_{-\infty}^{\infty} f(x) \delta(x)dx \nonumber \\ &=& \int_{-\varep}^{\varep} f(x) \delta(x)dx = f(0) \end{eqnarray} ただし、\(\varep\)は正の微小な数。
物理の問題では積分範囲が \begin{equation} \int_{-\infty}^{\infty} f(x) \delta(x-a)dx=f(a) \tag{\ref{delta}} \end{equation} のように\(-\infty ~ \infty\)であるとは必ずしも限りません。 そんな時はこの考え方が役に立ちます。
より一般的には以下の性質が成り立ちます。
デルタ関数について以下が成り立つ。 \begin{eqnarray} \int_{-\infty}^{a-\varep} f(x) \delta(x-a)dx &=& 0 \\ \int_{a+\varep}^{\infty} f(x) \delta(x-a)dx &=& 0 \\ \int_{a-\varep}^{a+\varep} f(x) \delta(x-a)dx &=& f(a) \\ \end{eqnarray} ただし、\(\varep\)は\(0\)でない正の実数。
積分範囲に関する公式です。\(\delta(x-a)\)は\(x=a\)以外では\(0\) なので、積分範囲に\(a\)を含まない限り、どんな範囲で積分しても\(0\)になります。逆に、\(a\) を含む範囲なら、それが有限である限り値を返します。
合成関数のデルタ関数(レベル2)
デルタ関数について以下が成り立つ。 \begin{equation} \label{compositedelta} \delta(f(x))= \sum_{i}{1 \over |f'(a_{i}) |} \delta(x-a_{i}) \end{equation} ただし、\(a_{i}\)は\(i\)番目の\(f(x)\)が\(0\)になる点で、和はそれが複数ある場合に取る。\(f'(a_{i})\)は \(f(x)\)の導関数の\(a_{i}\)での値。
デルタ関数が合成関数になりました。複雑に見えますが、簡単な例を考えると感覚が掴みやすいです。 例えば\(f(x)=ax\)として選ぶと、\(f(x)=0\)になる点は\(x=0\)しかないため和は不要であって \begin{equation} \delta(ax)= {1 \over |f'(a_{1}) |} \delta(x-a_{1}) \end{equation} また今回は\(a_{1}=0\)で、\(f'(0)=a\)なので \begin{equation} \delta(ax)= {1 \over |a|} \delta(x) \end{equation} になります。これは定数倍の時の式(\ref{atimesdelta})に一致しています。
\(f(x)=0\)の点が複数ある例としては \(f(x)=x^2-a^2\)が有名です。これは\(f(\pm a)=0\)なので二つの点\(x=\pm a\)で 和を取る必要があります。結果を書くと以下のようになります。
\(a\)を\(0\)ではない正の実数とした時、デルタ関数について以下が成り立つ。 \begin{equation} \label{sqdelta} \delta(x^2-a^2)= {1 \over 2a} \Bigl \{ \delta(x-a) + \delta(x+a) \Bigr \} \end{equation}
これは\(|f'(\pm a)|=2a\)を(\ref{compositedelta})式に代入することで導けます。
これらの公式の証明は長くなるので、デルタ関数の公式(標準編)にまとめてあります。
デルタ関数の微分(レベル2)
デルタ関数の微分について、以下が成り立つ。 \begin{equation} f(x)\frac{d}{dx} \delta(x)=-\delta (x) f'(x) \end{equation} ここに、\(f'(x)\)は\(f(x)\)の導関数。
デルタ関数にも微分を定義することができます。証明は部分積分を使います。 詳しくはデルタ関数の公式(基本編)からどうぞ。
この公式を使えば、デルタ関数のテイラー展開を形式的に定義でき、 例えば\(\delta(x+a)\)を \(a\)が微小と思って展開すると \begin{eqnarray} f(x)\delta(x+a)&=&f(x)\Bigl\{\delta(x)+a\frac{d}{dx}\delta(x)+ \cdots \Bigr\} \nonumber \\ &=& \Bigl\{f(x)-\frac{d f(x)}{dx}a+ \cdots \Bigr\}\delta(x) \nonumber \\ &=& \Bigl\{f(0)-\frac{d f(0)}{dx}a+ \cdots \Bigr\}\delta(x) \end{eqnarray} のように変形できます。ちなみに、最終行右辺の中括弧の中身は\(f(-a)\)のテイラー展開になっているので 上の式は \begin{eqnarray} f(x)\delta(x+a) = f(-a)\delta(x+a) \end{eqnarray} と同値です。これはデルタ関数の持つ性質(\ref{deltaeq2})式そのものであり、 ちゃんとデルタ関数のテイラー展開が矛盾なく機能していることがみてとれます。
デルタ関数のテイラー展開は物理ではそこそこ使います。特に、デルタ関数の引数が複雑だったり、多変数の時は 特に有効です。
多変数の場合(3次元,極座標など)(レベル2)
物理で使うデルタ関数は(\ref{delta})式のように1次元であることはまれであり、3次元または2次元である ことが多いです。また、多次元で考えるとおのずと変数も増えるので多変数になります。ここでは多変数の場合のデルタ関数について簡単に確認します。
\(\delta^3(\bs{x})\)は3次元のデルタ関数であり、その意味は デカルト座標において \begin{equation} \label{3ddelta} \delta^3(\bs{x}-\bs{X})=\delta(x-X)\delta(y-Y)\delta(z-Z) \end{equation} である。
物理でよく目にする表式です。ベクトルが引数になっていて初見だと戸惑うかもしれませんが、これはデカルト座標 の場合\(\bs{x}=(x,y,z),\bs{R}=(X,Y,Z)\)の略記であって、その意味は(\ref{3ddelta})式の右辺であることに注意してください。 同様に2次元の場合は \begin{equation} \delta^2(\bs{x}-\bs{X})=\delta(x-X)\delta(y-Y) \end{equation} のようになります。いずれの場合も、各成分ごとのデルタ関数は1次元と同じ性質を示します。また、 全空間で積分すると \begin{eqnarray} & & \int \mathrm{dV} \delta^3(\bs{x}-\bs{X}) \nonumber \\ &=&\int_{-\infty}^{\infty} \mathrm{dx} \int_{-\infty}^{\infty} \mathrm{dy} \int_{-\infty}^{\infty} \mathrm{dz} \delta(x-X)\delta(y-Y)\delta(z-Z) \nonumber \\ &=&1 \end{eqnarray}
のように\(1\)になります。極座標の場合、デルタ関数は \begin{equation} \delta^3(\bs{x}-\bs{X})=\frac{1}{r^2 \sin \theta}\delta(r-R)\delta(\theta-\Theta)\delta(\phi-\Phi) \end{equation} である。
極座標の場合の表式です。前に係数\(r^2 \sin \theta\)が付いている理由は極座標変換すると、 \begin{eqnarray} 1&=& \int_{-\infty}^{\infty} \mathrm{dx} \int_{-\infty}^{\infty} \mathrm{dy} \int_{-\infty}^{\infty} \mathrm{dz} \delta^3(\bs{x}-\bs{X}) \nonumber \\ &=& \int_{0}^{\infty} \mathrm{dr} \int_{0}^{\pi} \mathrm{d\theta}\int_{-\pi}^{\pi} \mathrm{d\phi}\ r^2 \sin \theta \delta^3(\bs{x}-\bs{X}) \end{eqnarray} (極座標の積分範囲に注意) のようにヤコビアンが出てくるので、それを打ち消すためです。定数倍(\ref{atimesdelta})式の時と同じ理由ですね。
2変数関数\(f(x,y)\)に対し \begin{eqnarray} & & \int_{-\infty}^{\infty} dx \int_{-\infty}^{\infty} dy f(x,y) \delta(x-a+y-b) \nonumber \\ &=& \int_{-\infty}^{\infty} dy f(a-y+b,y) \nonumber \\ \Bigl(&=& \int_{-\infty}^{\infty} dx f(x,b-x+a) \Bigr) \end{eqnarray} が成り立つ。
(\ref{delta})式で、\(a\)が定数ではなく、変数を含む場合も考えることができます。 その場合でも、普通のデルタ関数と同じように引数が\(0\)、つまり\(x=a-y+b\)の時 ピークが立ち、それ以外ではデルタ関数は値が\(0\)になるので、上の式のようになります。