楕円の標準形
以下の方程式は楕円を表す \begin{equation} \label{standardtype} \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \end{equation} これを楕円の標準形と呼ぶ
楕円を数式で表す時の基本形です。\(a,b\)の大小によって、横長の楕円か縦長の楕円を表すかが変わります。
楕円の定義や性質について詳しくは→楕円とその諸性質からどうぞ。
楕円の標準形について簡単にまとめました。
導出(レベル1)
楕円の定義を使って標準形を導きます。まずは定義をおさえておきましょう。
2定点からの距離の和が一定となるような点の軌跡 を楕円と呼ぶ。
この二定点のことを焦点と呼びます。
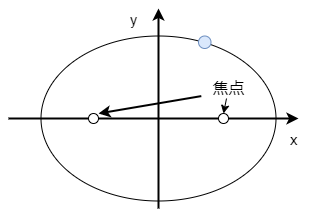
その他導出には楕円の性質を使います。詳しくは楕円とその諸性質 を参照してください。
導出
焦点の座標をそれぞれ\((c,0),(-c,0)\)と置く。すると、楕円上のある点の座標を\((x,y)\)と置けば 焦点からの距離を\(x,y\)を使って計算することができる。 また、楕円の性質により、この距離の合算値は長軸の長さ\(2a\)に等しく、 \begin{equation} \sqrt{(x+c)^2+y^2}+\sqrt{(x-c)^2+y^2}=2a \end{equation} である。
これを計算して(\ref{standardtype})式を導く。まずは移行して \begin{equation} \sqrt{(x+c)^2+y^2}=2a-\sqrt{(x-c)^2+y^2} \end{equation} 両辺二乗する。 \begin{eqnarray} & \ &(x+c)^2+y^2 \nonumber \\ &=&4a^2-4a\sqrt{(x-c)^2+y^2}+(x-c)^2+y^2 \end{eqnarray} これを整理すると \begin{equation} a\sqrt{(x-c)^2+y^2}=a^2-cx \end{equation} となる。これをさらに二乗する。 \begin{eqnarray} &a^2& \{(x-c)^2+y^2 \} \nonumber \\ &=&a^4-2a^2 cx +c^2x^2 \end{eqnarray} これを整理すると \begin{eqnarray} (a^2-c^2)x^2+a^2y^2=a^2(a^2-c^2) \end{eqnarray} が得られ、両辺\(a^2(a^2-c^2)\)で割り、 最後に短軸の長さを\(b\)と置くと、\(b^2=a^2-c^2\)が成り立つので これを適用すると \begin{equation} \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \tag{\ref{standardtype}} \end{equation} が得られた。
媒介変数表示(レベル1)
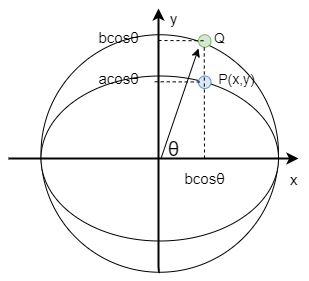
楕円の媒介変数表示は \begin{eqnarray} \begin{cases} x =a \cos \theta \\ y= b \sin \theta \end{cases} \end{eqnarray} である。
媒介変数表示とは、上の条件を満たす\((x,y)\)をあらゆる\(\theta\)について プロットすると、楕円が書けるということです。楕円を線積分するときなどに使えます。
半径が\(b\)の円の媒介変数表示が \begin{eqnarray} \begin{cases} x =b \cos \theta \\ y= b \sin \theta \end{cases} \end{eqnarray} であることと比較すると、楕円が円を\(x\)方向に\(\frac{a}{b}\)伸ばした図形であることが見て取れると思います。
注意として、楕円の場合、媒介変数\(\theta\)は円の場合と違って、楕円上の点\((x,y)\) と原点とのなす角度とは何の関係もありません。(下図でいうと、\(P\)ではなく\(Q\)と原点の なす角が\(\theta\)であるということ)