楕円とその諸性質
2定点からの距離の和が一定となるような点の軌跡 を楕円と呼ぶ。
楕円とは冒頭の通り、二定点(これを焦点と呼ぶ) からの距離が等しい点(例えば、下図の青点)の集まりの図形のことをいいます。
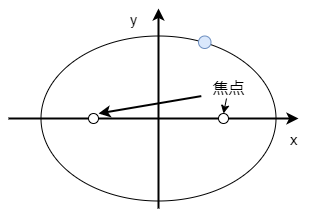
楕円は万有引力のところでよく使います。楕円の性質について簡単にまとめました。
具体例(レベル1)
例えば、 \begin{equation} \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \quad (a>b) \end{equation} は横長の楕円を表し、図示すると以下の通り。

この場合、長軸は\(2a\)、短軸は\(2b\)である。(長軸短軸については後述)
同様に \begin{equation} \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \quad (b>a) \end{equation} は縦長の楕円を表し、図示すると以下の通り。
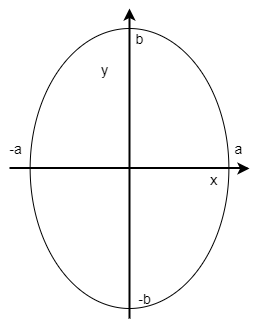
この場合、長軸は\(2b\)、短軸は\(2a\)である。(長軸短軸については後述)
数式での表示(レベル1)
楕円はデカルト座標では \begin{equation} \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \end{equation} の形でかける。これを標準形と呼ぶ
デカルト座標における楕円の表示です。円の方程式と見比べると、 円を縦横に異なる比率で引き延ばした図形が楕円、ということが見て取れます。
ちなみに、\(a\)や\(b\)はそれぞれ長軸と短軸の半分の値に対応します。 詳しくは楕円の標準形を参照してください。
楕円は極座標では \begin{equation} r=\frac{l}{1+\epsilon \cos \theta} \end{equation} の形でかける。ただし、\(0 < \epsilon <1 \)
楕円の極座標表示です。この表示は\(\epsilon\)の大小で、 異なる二次曲線も表せます。詳しくは、二次曲線の極座標表示を参照。
性質(レベル1~2)
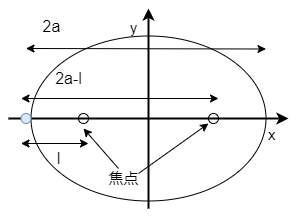
楕円上の点から、2焦点までの距離の和は 一定であり、その値は長軸の長さ\(2a\)に等しい。
長軸とは、楕円内部にひいた2焦点を通る直線のことです。 (上の具体例を見た方が分かりやすい) 前半部分は楕円の定義より自明ですが、なぜこれが\(2a\)に等しいか 説明します。
証明
楕円上の点のうち、以下の点を考える。
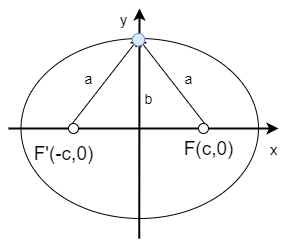
長軸の長さを\(2a\)、短軸の長さを\(2b\)とした時、 原点から焦点までの距離\(c\)は \begin{equation} \label{focallength} c=\sqrt{a^2-b^2} \end{equation} である。
長軸が、楕円内部にひいた2焦点を通る直線 なのに対し、短軸は楕円内部にひいた長軸の 垂直二等分線のことです。
証明
楕円上の点のうち、以下の点を考える。
楕円の面積\(S\)は長軸の長さを\(2a\)、短軸の長さを\(2b\)と置くと \begin{equation} S=\pi ab \end{equation}
楕円が円を引き延ばしたものと考えると、 この公式もイメージがしやすいと思います。真面目に定積分を 行っても、導出はできます。
証明
楕円の標準形 \begin{equation} \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \end{equation} について両辺\(b^2\)をかけると \begin{equation} \frac{b^2}{a^2} x^2+y^2=b^2 \end{equation} となるが、これはこの楕円が以下の円 \begin{equation} x^2+y^2=b^2 \end{equation} を\(x\)方向に\(\frac{a}{b}\)だけスケール変換したものだと 考えることができる。
この変換によって、面積は\(\frac{a}{b}\)になるので 楕円の面積は \begin{equation} S=\pi b^2 \frac{a}{b}=\pi ab \end{equation} と分かる。
楕円の片方の焦点に注目する。この焦点について、 近日点までの長さを\(R_{1}\)、遠日点までの長さを\(R_{2}\) と置くと、 \begin{eqnarray} \label{perihelion1} a&=&\frac{1}{2}(R_{1}+R_{2}) \\ \label{perihelion2} b&=&\sqrt{R_{1}R_{2}} \\ \label{perihelion3} c&=&\frac{1}{2}(R_{1}-R_{2}) \end{eqnarray} が成り立つ。ただし、長軸の長さを\(2a\)、短軸の長さを\(2b\) 原点から焦点までの距離を\(2c\)と置いた。
楕円特有の公式です。導出は近日点と遠日点を参照してください。
楕円の片方の焦点に注目する。この焦点から、楕円上のあらゆる点 までの距離の平均値は長半径\(a\)に等しい。
円の場合、焦点(すなわち中心)から円弧上までの距離 は一定ですが、楕円の場合は変化します。しかし、その平均値は 長半径(長軸の半分)によって表せます。
証明
楕円上のある点(下図の青点)を考える。この点について点対称な点が 楕円上に存在する。(下図の緑点)

さて、まずはこの二点のみに注目し、焦点からの平均距離を考える。 一方からの距離が\(L\)ならば、対称性と楕円の性質より、もう片方から の距離は\(2a-L\)であって、平均距離は\(a\)である。
楕円上の任意の点について、同じように点対称のペアを考えて計算 できる。楕円の点対称な図形なので、その全結果の平均を取れば、それは 楕円上のあらゆる点から焦点までの平均距離に等しく、その値は\(a\)である。
以上により示された。