近日点と遠日点
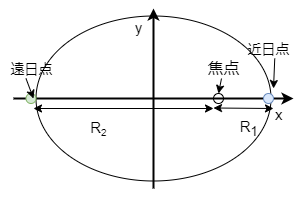
片方の焦点に注目する。楕円上の点のうちその焦点に最も近づく点を 近日点と呼び、最も遠くなる点を遠日点と呼ぶ
惑星の軌道を考えるうえで、近日点と遠日点は大事です。この二つの点について簡単にまとめました。
楕円の定義や性質について詳しくは楕円とその諸性質を参照してください。
性質(レベル1)
片方の焦点の近日点はもう片方にとっての焦点の遠日点。同様に片方の焦点の遠日点は もう片方の近日点
図を見れば当たり前の話です。楕円の対称性からも明らかです。
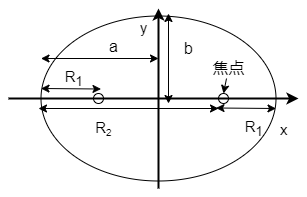
楕円の片方の焦点に注目する。この焦点について、 近日点までの長さを\(R_{1}\)、遠日点までの長さを\(R_{2}\) と置くと、 \begin{eqnarray} \label{perihelion1} a&=&\frac{1}{2}(R_{1}+R_{2}) \\ \label{perihelion2} b&=&\sqrt{R_{1}R_{2}} \\ \label{perihelion3} c&=&\frac{1}{2}(R_{1}-R_{2}) \end{eqnarray} が成り立つ。ただし、長軸の長さを\(2a\)、短軸の長さを\(2b\) 原点から焦点までの距離を\(2c\)と置いた。
近日点及び遠日点と、その他の楕円に関する長さの関係式です。基本となる公式なので おさえておきましょう。
証明
まず、(\ref{perihelion1})式については図2より明らかに \begin{equation} 2a=(R_{1}+R_{2}) \end{equation} なので言えた。続いて(\ref{perihelion3})式について これも、もう片方の焦点の位置に注目すると2焦点間の距離\(2c\)は \begin{equation} 2c=(R_{2}-R_{1}) \end{equation} と書けるので成り立つ。最後に(\ref{perihelion2})式は、 \(a,b,c\)の間に成り立つ関係式\(b^2=a^2-c^2\)より(証明はこちらを参照)、ここに (\ref{perihelion1})式と(\ref{perihelion3})式を代入することで 確認できる。
楕円の片方の焦点に注目する。この焦点について、 近日点までの長さを\(R_{1}\)、遠日点までの長さを\(R_{2}\) と置くと、 \begin{eqnarray} \label{aphelion} R_{2}&=&a(1+e) \\ \label{perihelion} R_{1}&=&a(1-e) \end{eqnarray} が成り立つ。ただし、長軸の長さを\(2a\)、短軸の長さを\(2b\) と置き、以下に定義される離心率\(e\)を使った。 \begin{equation} e=\frac{\sqrt{a^2-b^2}}{a} \end{equation}
近日点と遠日点の離心率を用いた表記です。 近日点と遠日点はこの形で出てくることが多いです。離心率については、 二次曲線の極座標表示も合わせて見てみてください。
証明
(\ref{perihelion1})式と(\ref{perihelion2})式より、 \begin{eqnarray} (R_{1}+R_{2})&=&2a \\ R_{1}R_{2}&=&b^2 \end{eqnarray} が成り立つ。和と積が分かっているので、ここで二次方程式の解と係数の関係を使い、 さらに\(R_{1} < R_{2}\)を考慮に入れると \begin{eqnarray} R_{2}&=&(a+\sqrt{a^2-b^2}) \\ R_{1}&=&(a+\sqrt{a^2-b^2}) \end{eqnarray} と分かる。ここで定数\(e\)を\(e=\frac{\sqrt{a^2-b^2}}{a}\)と定義すれば、 (\ref{aphelion})式と(\ref{perihelion})式が得られた。