コンプトン散乱
結晶に光(X線)を当てるとより波長の長い光が散乱される。散乱前後の波長の変化は散乱される角度\(\theta\)に依存し
\begin{equation}
\label{Compton}
\Delta \lambda = \frac{h}{m_{e} c}(1-\cos \theta)
\end{equation}
となる。(ただし、\(h\)はプランク定数、\(m_e\)は電子の質量)
この効果をコンプトン効果と呼び、この散乱をコンプトン散乱と呼ぶ。
高校物理でもおなじみのコンプトン散乱です。 有名な(\ref{Compton})式ですが、導出にはコツがいります。また、大学物理では相対論的な表式を使うので少し勝手が異なります。 コンプトン散乱について簡単にまとめました。
光量子仮説による説明(レベル1)
コンプトン散乱とは電子と光子の非弾性散乱と解釈できる。光子の波長はエネルギーと関連づくため、 散乱によって波長が変化する。
コンプトン散乱は古典的には説明が困難でしたが、量子論を使うことで自然な解釈が可能になりました。 光量子仮説では、光は光子という粒子の集まりとみなします。すると、もし光を結晶に照射すれば、電子と光子が衝突し 非弾性散乱を起こすだろうと想像がつきます。
光量子仮説では、光は\(E = h \nu\)のエネルギーを持つ光子として解釈されるのでした。 一方、光は波としての性質(干渉など)を併せ持つので、波の公式\(c = \nu \lambda\)が成り立つとしてみましょう。 すると、 \begin{eqnarray} \label{photon} E = h \nu = h\frac{c}{\lambda} \end{eqnarray} のようにエネルギーと波長が関連づくことがわかります。
非弾性散乱によって、散乱された光はエネルギーが変化しています。そして、その変化は散乱角に依存します。 エネルギーが変化すると、(\ref{photon})式より、波長\(\lambda\)も変化するので、(\ref{Compton})式 のような現象が起こると解釈できるのです。
波長の変化(レベル1)
結晶に光(X線)を当てるとより波長の長い光が散乱される。この時波長の変化は散乱される角度\(\theta\)に依存し、 \begin{equation} \Delta \lambda = \frac{h}{m_{e} c}(1-\cos \theta) \tag{\ref{Compton}} \end{equation} が成り立つ。
コンプトン散乱におけるコンプトン効果を表す式です。静止している電子にX線を照射した場合、 (\ref{Compton})式が成り立ちます。 静止していない電子の場合は(\ref{Compton})式の拡張が必要ですが、結晶に含まれる電子は静止しているので、 (\ref{Compton})式を知っていれば十分です。
以下では(\ref{Compton})式を導出します。その前に、光子のエネルギーと運動量の表式を確認しておきましょう。
光子は以下のエネルギーと運動量を持つ粒子として振舞う。 \begin{eqnarray} E &=& h \nu = h\frac{c}{\lambda} \\ p &=& \frac{h \nu}{c} =\frac{h}{\lambda} \end{eqnarray} ただし、二つ目のイコールで波の公式\(c = \nu \lambda\)を使った。
これらの公式の導出は光量子仮説の記事を確認してください。また、高校物理とは 違い、電子のエネルギーとして相対論的な表式 \begin{eqnarray} E &=& \sqrt{m_{e}^2c^4+p^2 c^2} \end{eqnarray} を使うことにします。このもとで、静止している電子のエネルギーは\(m_{e}c^2\)です。
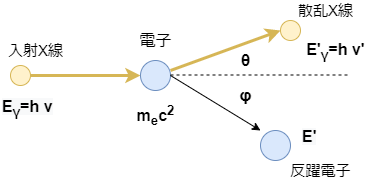
導出
図1を参考に、エネルギーと運動量保存則を連立すれば出せます。式変形の際、 \(\frac{1}{\lambda}\)の分母をそのまま残した方が楽に計算が進みます。
静止している電子に光子が衝突した状況を考える。図1のように、角度\(\theta\)、\(\phi\)を定める。 また、入射及び散乱X線のエネルギーをそれぞれ\(E_{\gamma}=h \nu,E'_{\gamma} = h \nu'\)と置く。 さらに電子の質量を\(m_{e}\)とし、衝突後のエネルギーと運動量の大きさをそれぞれ\(E',p\)と置く。
エネルギー保存の式は \begin{equation} h \nu -h \nu' = E' - m_{e}c^2 \end{equation} となる。入射X線方向の運動量保存則は \begin{equation} \frac{h \nu}{c} -\frac{h \nu'}{c} \cos \theta = p \cos \phi \end{equation} であって、入射軸に垂直な方向の運動量保存則より \begin{equation} \frac{h \nu'}{c} \sin \theta = p \sin \phi \end{equation} を得る。
欲しいのは波長の関係式だったので、これらの式を\(\lambda\)を使って書き換える。 その後式を並べると \begin{eqnarray} \label{econ} &&\frac{hc}{\lambda} -\frac{hc}{\lambda} = E' - m_{e}c^2 \\ &&\frac{h }{\lambda} -\frac{h}{\lambda'} \cos \theta = p \cos \phi \\ &&\frac{h}{\lambda'} \sin \theta = p \sin \phi \\ \end{eqnarray} である。
まずは、運動量保存則の二つの式をそれぞれ二乗し、和を取ると、 \begin{eqnarray} &&\Bigl(\frac{h}{\lambda} -\frac{h}{\lambda'} \cos \theta \Bigr)^2 + \Bigl(\frac{h}{\lambda'} \sin \theta \Bigr)^2 \nonumber \\ &&= p^2 \Bigl(\sin^2 \phi + \cos^2 \phi \Bigr) \end{eqnarray} から \begin{eqnarray} &&\Bigl(\frac{h}{\lambda}\Bigr)^2 +\Bigl(\frac{h}{\lambda'}\Bigr)^2 -2\frac{h}{\lambda}\frac{h}{\lambda'} \cos \theta \nonumber \\ \label{pcon} &&= p^2 \end{eqnarray} となって\(\phi\)を消去できる。
次に(\ref{econ})式を使いやすいように(\ref{pcon})式を \begin{eqnarray} && \Bigl (\frac{h}{\lambda}-\frac{h}{\lambda'} \Bigr)^2 +2\frac{h}{\lambda}\frac{h}{\lambda'} (1-\cos \theta) \nonumber \\ \label{pcon2} &&= p^2 \end{eqnarray} のように変形しておこう。ここで(\ref{econ})式より \begin{equation} \label{econ2} \Bigl(\frac{h}{\lambda}-\frac{h}{\lambda'} \Bigr)^2 = p^2 - 2\Bigl (\frac{h}{\lambda}-\frac{h}{\lambda'} \Bigr)m_{e}c \end{equation} という関係式が成り立つ。なぜなら \begin{eqnarray} && \Bigl(\frac{hc}{\lambda}-\frac{hc}{\lambda'} \Bigr)^2 \nonumber \\ &&= (E'-m_{e}c^2)^2 \nonumber \\ &&= E'^2 -2E' m_{e}c^2 +(m_{e}c^2)^2 \nonumber\\ &&= E'^2 -(m_{e}c^2)^2 -2(E' - m_{e}c^2)m_{e}c^2 \nonumber\\ &&= p^2 c^2 -2\Bigl (\frac{hc}{\lambda}-\frac{hc}{\lambda'} \Bigr)m_{e}c^2 \end{eqnarray} のように書き換えられるからである。ただし、最終行で相対論的なエネルギーの関係式 \(E^2=m_{e}^2c^4+p^2c^2\)を使った。
(\ref{econ2})を(\ref{pcon2})式に代入し、\(p^2\)を消去する。
\begin{eqnarray} && - 2\Bigl (\frac{h}{\lambda}-\frac{h}{\lambda'} \Bigr)m_{e}c+2\frac{h}{\lambda}\frac{h}{\lambda'} (1-\cos \theta) \nonumber \\ &&= 0 \end{eqnarray} 最後に両辺に\(\lambda \lambda'\)をかけて分母をはらって変形すれば \begin{equation} \lambda'-\lambda = \frac{h}{m_{e} c}(1-\cos \theta) \end{equation} を得る。これは(\ref{Compton})式にほかならない。
エネルギーの変化(レベル2)
結晶にX線を照射した時、散乱後のX線のエネルギー\(E'_{\gamma}\)は 入射時のエネルギー\(E_{\gamma}\)を用いて \begin{equation} \label{energy} E'_{\gamma}=\frac{E_{\gamma}}{1+(1-\cos \theta)\frac{E_{\gamma}}{m_{e}c^2}} \end{equation} で与えられる。
コンプトン散乱におけるエネルギーの変化です。\(1-\cos \theta \geq 0\)より、 (\ref{energy})式の右辺の分母は\(1\)以上です。このため\(E_{\gamma} \geq E'_{\gamma}\)が成り立ちます。 (等号成立は\(\cos \theta =1\)の時。)
導出
(\ref{Compton})式より \begin{equation} \lambda'-\lambda = \frac{h}{m_{e} c}(1-\cos \theta) \end{equation} であるが、ここに光子のエネルギーの公式 \begin{equation} E_{\gamma} = h \nu = h\frac{c}{\lambda} \end{equation} を使えば、 \begin{equation} \frac{1}{E'_{\gamma}}-\frac{1}{E_{\gamma}}= \frac{1}{m_{e}}(1-\cos \theta) \end{equation} と変形できる。(ただし、\(E'_{\gamma}= \frac{hc}{\lambda'}\)である)
両辺\(E_{\gamma}\)を掛けて変形すると、 \begin{equation} \frac{E_{\gamma}}{E'_{\gamma}}= 1+\frac{E_{\gamma}}{m_{e}}(1-\cos \theta) \end{equation} のようになり、あとは両辺逆数をとって再び両辺\(E_{\gamma}\)を掛ければ \begin{equation} E'_{\gamma}=\frac{E_{\gamma}}{1+(1-\cos \theta)\frac{E_{\gamma}}{m_{e}c^2}} \tag{energy} \end{equation} を得る。