量子ゆらぎ
位置や運動量のように、実験によって観測可能な量を物理量と呼ぶ。 量子状態の物理量を観測したとき、全く同じ条件で、全く誤差のない計測を行ったとしても、 一般にはその観測値はばらつく。この不確定性を量子ゆらぎとよぶ。
量子ゆらぎとは、量子力学の根底にある概念です。ミクロなスケールでは、 全く同じ実験を全く誤差なく行うことができたとしても、一般にはその実験結果はばらつくということです。 量子ゆらぎについて簡単にまとめました。
具体例(レベル2)
具体例を通して、まずは量子ゆらぎのイメージを(なんとなくでよいので)掴みましょう。
具体例その1(ドブロイ波の位置)
ドブロイ波の記事でも述べたように、物質波は以下のような波束として解釈される。この波束の「位置」を 誤差なく測定した場合を考える。
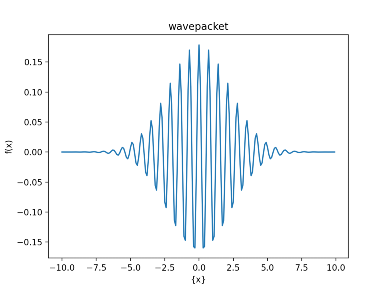
質点のように、大きさのない粒子であれば、その点こそが粒子の「位置」であるが、 波束は図1のように広がりを持つため、位置の定義が質点ほど自明ではない。
実は、この波束の広がりこそが、位置を測定した時の物質波の量子ゆらぎに対応する。 つまり、位置の測定値は、波束が振幅を持つ範囲の中でばらつき、一意に定まらない。 これを位置の不確定性(または不定性)と呼ぶ。
現実の具体例として、原子に束縛された電子の位置の不確定性は、原子の大きさに大体等しいという事実がある。 つまり、電子が原子中のどの地点に存在するかは測定の度に変化するが、そのばらつきは原子の中に収まる。
ドブロイ波の位置の観測値は、誤差のない完璧な測定を行ったとしても、ある一定の範囲内においてばらつきます。 この不確定性は、粒子が一点ではなく、波束のように広がりを持つためだと解釈できます。
具体例その1(回折現象と運動量)
物質波の運動量を考える。ドブロイ波の記事で触れたように \begin{equation} \label{pandk} \bs{p}=\hbar \bs{k} \end{equation} だから、波の進行方向が運動量の方向に対応する。
さて、直進する波をスリットに通すと、直後に回折を起こすことが知られている。 この時、波は同心円状に広がるが、(\ref{pandk})式よりこれは運動量の方向が同心円状にゆらいだことを意味する。
ドブロイ波は位置だけでなく、運動量もゆらぎます。以上の例を踏まえてわかることは、 量子ゆらぎとは、物質波の持つ波としての性質によって発生する性質だということです。後述する不確定性原理も 物質波が波としての性質を持つ限り、破ることができない原理になっています。
具体例その3(光の偏光)
光の偏光を考えよう。光の偏光には様々な種類があるが、偏光板を使えば特定の偏光 のみを取り出すことができる。光の進行方向を\(z\)軸にとったとき、\(x\)軸にそった偏光のみ 通過できる偏光板\(X\)を用意したとしよう。
当然、\(x\)軸に沿った偏光を持つ光子が飛んで来れば、その光子は偏光板\(X\)を通過できるが \(y\)軸に沿った偏光を持つ光子の場合は、偏光板\(X\)を通過することができない。
今、光子の波としての性質を使い、\(x\)軸に沿った偏光の状態と、\(y\)軸に沿った偏光の状態を 重ね合わせた量子状態を作ったとする。この光子をたくさん用意して、一個ずつ偏光板\(X\)にぶつけて通過できるか調べる。
結論から言うと、結果は光子によって通過できたり、できなかったりとばらつく。 すなわち、全く同じ光子を用意して、同じ実験を行っても、確率的に結果がばらつくのである。
量子ゆらぎによってゆらぐのは、位置や運動量だけではありません。 その中で特に有名な例として、ここでは光の偏光を挙げました。この例は少し難しいため、今は そういうものもあるのか、程度に思ってもらえるとよいです。
不確定性原理(レベル2)
量子状態の位置や運動量には量子ゆらぎ(不確定性)があるため、同時に両者を決定する ことはできない。位置、運動量の量子ゆらぎをそれぞれ\(\delta x,\delta p\)と 置いたとき、両者の積には以下の下限が存在する。 \begin{equation} \label{uncertaintyP} \delta x \ \delta p \geq \frac{\hbar}{2} \end{equation} この不等式を不確定性原理と呼ぶ。波動関数(量子状態)によって 位置、運動量の量子ゆらぎ\(\delta x,\delta p\)の値は異なり、 特に(\ref{uncertaintyP})式の等号が成立する場合、最小不確定性と呼ぶ。
有名なハイゼンベルクの不確定性原理です。量子ゆらぎ\(\delta x, \delta p\)の厳密な定義 や、導出は後の記事で行うとして、ここではこの式(\ref{uncertaintyP})の意味について簡単に解説します。
(\ref{uncertaintyP})式は一言でいえば、位置、運動量の決定精度の下限を決める不等式です。 実際(\ref{uncertaintyP})式は、位置と運動量のゆらぎが同時に\(0\)になる状況(\(\delta x = \delta p =0\))を禁止しています。 このため、しばしば量子状態は位置と運動量を同時に決定することはできない、と説明されます。
さらに、位置のゆらぎ\(\delta x\)が\(\hbar/2\)くらいに小さい時、運動量のゆらぎは \(\delta p\)は\(1\)より大きくなければなりません。逆もまたしかりです。以上をまとめると、 (\ref{uncertaintyP})式は\(\delta x, \delta p\)の両方を同時に\(\hbar/2\)より小さくできないことを意味します。
具体例(回折と不確定性原理)
具体例を見て、不確定性原理のイメージをつかみましょう。
直進する波をスリットに通すと、直後に回折を起こすことが知られている。 今、スリットの幅を\(\Delta x\)程度にとったとする。不確定性原理より、スリットを通過 した直後の運動量の不確定性\(\Delta p\)は \begin{equation} \Delta p \geq \frac{\hbar}{2\Delta x} \end{equation} で与えられる。これは、スリットの幅\(\Delta x\)を小さくすると、 それに反比例して運動量の不確定性\(\Delta p\)の下限が増加することを意味する。 実際幅の狭いスリットを通した時のほうが、回折効果が強く表れ、波はより広く広範に伝搬する。
不確定性の説明としてよく使われるスリットの例です。等速直線運動をする質点を スリットに通すと、位置と運動量を同時に決定できますが、物質波の場合はスリットを通過した 瞬間に波としての性質で 運動量がゆらいぐので、位置と運動量を同時には決められません。