物質波(ドブロイ波)
あらゆる粒子は波動的な性質を併せ持つ。 その波長は \begin{equation} \label{DeBroglie} \lambda = \frac{h}{p} \end{equation} で与えられる。このような波を物質波と呼ぶ。 ただし、\(h\)はプランク定数と呼ばれる定数。
光量子仮説を契機に、波と思われていた光に粒子の性質があることが発覚しました。 ドブロイは、電子等の粒子は逆に、波の性質を持つのではないかと考え (\ref{DeBroglie})式を導入しました。この波長を持った物質を、物質波(またはドブロイ波)と呼びます。 物質波について簡単にまとめました。
例題(レベル1)
例題を通して直感を養いましょう。
例題その1
時速\(90\)kmで飛んでいる野球ボールのドブロイ波長を求めたい。ただし野球ボールの質量を\(100\)gとする。
野球ボールの運動量は\(p = mv\)で表せる。ゆえにドブロイ波長は (\ref{DeBroglie})式から以下のように書ける。 \begin{eqnarray} \lambda = \frac{h}{p} = \frac{h}{mv} \end{eqnarray} ここに\(v = 90[\mathrm{km/h}] = \frac{90 \times 10^{3}}{360} [\mathrm{m/s}]\)と\(m = 0.1 [\mathrm{kg}]\)及び、\(h = 6.6 \times 10^{-34} [\mathrm{J \cdot s}]\)を 代入。\([J] = [\mathrm{kg \cdot m^2 \cdot s^{-2}}]\)に注意して \begin{eqnarray} \lambda &=& \frac{6.6}{0.1 \times 250} \times 10^{-34} [\mathrm{m}] \nonumber \\ &=& 2.6 \times 10^{-35}[\mathrm{m}] \end{eqnarray} を得る。
野球ボールの物質波です。波とは言っても波長が非常に短いので、日常生活では波として知覚することはできません。 原子核が大体\(1[\mathrm{fm}]= 1 \times 10^{-15}[\mathrm{m}]\)くらいなので、これよりはるかに小さいです。
また、物質波のイメージとして正しいのは、海の波のような平面波ではなく、後述するような「波束」です。 波長が十分短く、波束が十分局在すれば、それは粒子(あるいは質点)として振舞います。
例題その2
電子に電圧\(V = 10[\mathrm{V}]\)をかけたときのドブロイ波の波長を求めたい。
電子の運動量はエネルギー保存則 \begin{equation} \frac{p^2}{2m_{e}} = eV \end{equation} より、\(p = \sqrt{2m_{e}eV}\)である。 ドブロイ波長は(\ref{DeBroglie})式から \begin{equation} \lambda = \frac{h}{p} = \frac{h}{\sqrt{2m_{e}eV}} \end{equation} となる。後は具体的に値を入れて計算すればよい。
ここに\(V = 10 [\mathrm{V}]\)であって、その他の定数は\(e = 1.6 \times 10^{-19} [C],m_{e} = 9.1 \times 10^{-31}[\mathrm{kg}], h = 6.6 \times 10^{-34} [\mathrm{J \cdot s}]\) である。途中、\([J] = [\mathrm{C \cdot V}]\)を使えば、 \begin{eqnarray} \lambda &=& \frac{6.6}{\sqrt{20 \times 9.1 \times 1.6}} \times 10^{-9} [\mathrm{m}] \nonumber \\ &=& 3.9 \times 10^{-10}[\mathrm{m}] \end{eqnarray} を得る。
(別解)\([\mathrm{eV}]\)を使う計算
上ではSI単位系で計算したが、素粒子・原子核の分野では\(1[\mathrm{eV}] := e[\mathrm{V}]\)なる単位 \([\mathrm{eV}]\)(電子ボルト)をよく使う。ここで、 \begin{eqnarray} \lambda &=& \frac{h}{\sqrt{2m_{e}eV}} \nonumber \\ &=& \frac{2 \pi \hbar c}{\sqrt{2m_{e}c^2 eV}} \end{eqnarray} と変形する。ここで、本例題では\(V=10[V]\)であるからこれを代入する。 さらに、\(10e [\mathrm{V}]=10[\mathrm{eV}]\)及び、 電子の静止エネルギーの値\(m_{e}c^2 = 511 \times 10^{3}[\mathrm{eV}]\)と\(\hbar c = 1.97 \times 10^{-7}[\mathrm{eV \cdot m}]\) を用いると、。 \begin{eqnarray} \lambda &=& \frac{2 \pi \times 1.97}{\sqrt{2 \times 511}} \times 10^{-9} [\mathrm{m}] \\ &=& 3.9 \times 10^{-10}[\mathrm{m}] \end{eqnarray} となって、同じ結果を得る。(\([\mathrm{eV}]\)を使う時は、静止エネルギーを用いて計算すると楽。)
電子のドブロイ波長です。典型的な原子の大きさは大体\(1Å = 1 \times 10^{-10}[\mathrm{m}]\)と 言われているので、原子の大きさと同程度の波長の波というわけです。(野球ボールの例より 波長は長くなりましたが、当然目視ではみえません)
また、この波長は\(X\)線の波長(\(1 \times 10^{-8}[\mathrm{m}]~1 \times 10^{-11}[\mathrm{m}]\)) とも同じくらいなので、電子は\(X\)線と同じく結晶に照射すると回折現象を起こします。これの有名な実験に デビッソンとガーマーの実験があります。
エネルギーと運動量(レベル2)
物質波は以下のエネルギーと運動量を持つ。 \begin{eqnarray} \label{energy} E &=& h \nu \\ \label{momentum} p &=& \frac{h}{\lambda} \end{eqnarray} ただし、\(\nu\)は振動数であり、\(h,c\)はそれぞれプランク定数と 光速度。
物質波のエネルギーと運動量の公式です。大学物理ではディラック定数\(\hbar = \frac{h}{2\pi}\) を導入して \begin{eqnarray} E &=& \hbar \omega \\ p &=& \hbar k \end{eqnarray} と普通は書きます。ここに、角振動数\(\omega = 2 \pi \nu = \frac{2\pi}{T}\)と、波数\( k = \frac{2 \pi}{\lambda}\) を定義しました。波数は\(2 \pi\)あたりの波の個数のことで、角振動数と対になる概念です。\(2\pi\) とは単位円の長さのことで、単位円一周あたり波が何個入るかに相当します。
ちなみに、3次元の場合は\(p\)がベクトル\(\bs{p}\)に、\(k\)がベクトル\(\bs{k}\)になり \begin{eqnarray} \label{energy2} E &=& \hbar \omega \\ \label{momentum2} \bs{p} &=& \hbar \bs{k} \end{eqnarray} になります。
これらの表式は光量子仮説の時と全く同じです。今は、物質波も光子と同じ公式を満たすと仮定した と思えばよいです。もし、この\(E\)がニュートン力学のエネルギー\(\frac{\bs{p}^2}{2m}\)に等しいとすると、 \(E = \frac{\bs{p}^2}{2m} = \frac{\hbar^2 \bs{k}^2}{2m}\)になるため、 \begin{eqnarray} \omega &=& \frac{\hbar \bs{k}^2}{2m} \end{eqnarray} が得られます。このような角振動数と波数の関係を分散関係と呼びます。
より厳密な解釈(レベル2)
物質波は粒子の速度と同じ群速度\(v_{g}=\frac{p}{m}\)を持つ波束として解釈される。
物質波の解釈です。波のイメージとして海の波のような平面波を思い浮かべる人がいるかもしれませんが、 粒子的な描像を併せ持つ物質波のイメージとしては、波束がこれに該当します。
波束とは図1のような波のことで、平面波と比べて局在した波になっています。 わずかに異なる波長の平面波を重ね合わると、このような波になります。(これは音波のうなりと 同じです)
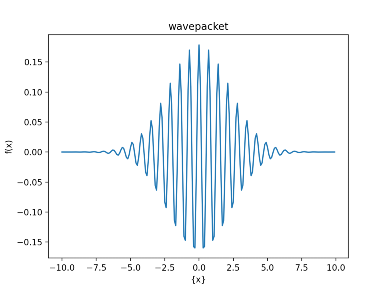
波束にはいろいろバリエーションが存在し、より局在した以下のような波束も あります。
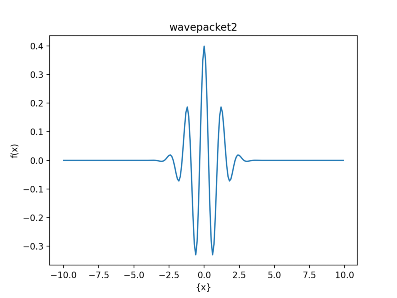
この局在した部分に粒子が存在していると思ってください。この波の振幅は
その地点に存在する確率を表しています。(詳しくは→確率密度による解釈)
粒子が動くと、この波束も動きます。この時の波束の速度を群速度と呼びます。(群速度について詳しくは→波束)
相対論的な場合(レベル3)
物質波のエネルギーと運動量の公式 \begin{eqnarray} E &=& \hbar \omega \tag{\ref{energy2}} \\ \bs{p} &=& \hbar \bs{k} \tag{\ref{momentum2}} \end{eqnarray} はローレンツ不変である。
上のセクションでエネルギーと運動量の表式を導入した際、光子と同じ表式を仮定しました。この仮定の正当性の一つが ローレンツ対称性です。仮に、物質波が相対論的な速度をもった時、(\ref{energy2})式や(\ref{momentum2})式が成り立っていれば、 相対性理論と矛盾せず、かつ波としての性質が説明できて嬉しいわけです。
解説
ここでは公式(\ref{energy2})式、(\ref{momentum2})式がローレンツ不変であることを説明します。「公式がローレンツ不変」 であるとは、公式が慣性系によらずに成り立つということです。
題意を示すには、左辺と右辺が同じローレンツ変換則に従うことがいえればよい。 左辺の\((E,\ \bs{p})\)は4元ベクトルより、右辺の\((\omega, \ \bs{k})\)も4元ベクトルとして振舞うことがいえれば、 これらの公式がローレンツ不変であることを示せたことになる。
今、波動関数\(\psi(\bs{r})\)を、 \begin{eqnarray} \psi(\bs{r},t) = \sum_{\bs{k},\omega} \psi(\bs{k},\omega) e^{i(\bs{k} \cdot \bs{x}-\omega t)} \end{eqnarray} のように平面波で展開したとする。ここで、位相\(\bs{k} \cdot \bs{x}-\omega t\)はローレンツ変換に 対して不変な量である。なぜなら、ある慣性系で節になっている時空点は、他の慣性系から見ても節になっている からである。(一般に、時空点(事象)は座標系によらず一意に決まります。)例えば、\(\bs{k} \cdot \bs{x}-\omega t = \frac{\pi}{2}\) はローレンツ不変。これの右辺はただの数なので、左辺もまたローレンツ不変な量になる。
\(\bs{k} \cdot \bs{x}-\omega t\)がローレンツ不変な量ならば、これは\((\omega, \ \bs{k})\)と\((t, \ \bs{x})\) の内積のような形をしているため、\((\omega, \ \bs{k})\)が4元ベクトルのように 振舞うべきであると言える。
以上より、\((\omega, \ \bs{k})\)が4元ベクトルとして振舞うことが示せた。 ゆえに公式(\ref{energy2})式、(\ref{momentum2})式はローレンツ不変である。
上の論理は物質波だけでなく、光子についても言えます。また、物質波について非相対論的極限を取ると \begin{eqnarray} E &=& mc^2 + \frac{1}{2}mv^2 \\ p &=& mv \end{eqnarray} になりますが、エネルギーの基準を\(mc^2\)が原点になるように取り直すと、 非相対論的な粒子についても \begin{eqnarray} E &=& \hbar \omega \tag{\ref{energy2}} \\ \bs{p} &=& \hbar \bs{k} \tag{\ref{momentum2}} \end{eqnarray} が成り立つと言えます。