波動関数と規格化
物質波を、位置\(x\)と時刻\(t\)の関数としてあらわしたものを波動関数\(\psi(x,t)\)と呼ぶ。 この関数は、図示すると波のように振舞う。
量子力学において基本概念となる波動関数です。上の説明では曖昧なので、 下で解釈と意味をきちんと確認します。量子力学における波動関数について簡単にまとめました。
具体例(レベル1)
具体例を通してイメージを養いましょう。最初は数式よりも、図と定義を交互に 見た方がわかりやすいと思います。
具体例その1
波動関数の一例として\(t=0\)の時に \begin{eqnarray} \label{wavepucket} \psi(x,0)= \frac{1}{\sqrt{10 \pi }} \exp \left[-\frac{x^2}{10}+ 9 \mathrm{i} x\right] \end{eqnarray} とかける場合がある。これは図示すると以下のようになる。

ただし、\(\psi(x,0)\)は複素関数なので図示したのは実部である。
図1(あるいは(\ref{wavepucket}))式)のように、ある地点に局在しているような波を波束といいます。 ドブロイ波の記事でも述べたように、物質波は基本的には波束として解釈されます。 丁度、他より波高が高くなっている部分に粒子が存在しているイメージです。
具体例その2
波動関数の一例として\(t=0\)の時に \begin{eqnarray} \label{planewave} \psi(x,0)= \frac{1}{\sqrt{2 \pi}} e^{2i x} \end{eqnarray} とかける場合がある。これは図示すると以下のようになる。
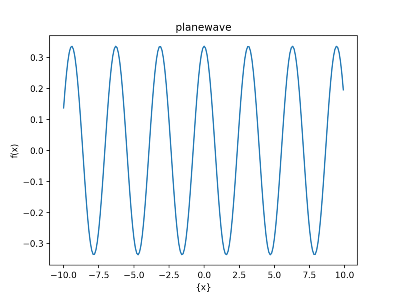
ただし、\(\psi(x,0)\)は複素関数なので図示したのは実部である。
図2(あるいは(\ref{planewave})式)のように、一様に広がった波を平面波といいます。\(\sin x\)や、\(\cos x\)など も平面波の一種です。数学的に平面波は扱いやすいので、量子力学では平面波がよくでてきます。
例1の波束は粒子的な解釈ができますが、平面波にはそれができません。平面波は一様に広がっているため特別な場所がなく、 粒子という局在的な描像とは相性が悪いからです。このあたりの問題については後で記事をかきます。
(\ref{wavepucket})式や(\ref{planewave})式の形以外にも、様々な波動関数が存在します。 それらについては、シュレディンガー方程式を学んでいく中で紹介していく予定です。
確率密度による解釈(レベル2)
波動関数\(\psi (x,t)\)はその絶対値の二乗が存在確率の密度を表す。 つまり、時刻\(t\)に\(x \sim x+\Delta x \)の間に粒子が存在する確率を\( P(x,t)\)とした時、 それは \begin{eqnarray} \label{probability} P(x,t) = \int^{x+\Delta x}_{x} |\psi (x,t)|^2 dx \end{eqnarray} で与えられるということ。ただし、\(\Delta x\)は十分小さいとする。
波動関数の物理的解釈です。この式だけだとイメージがしづらいと思いますが、例えば具体例その1の 図1をみると、\(x=0\)のあたりで波の高さが高くなっていることがわかります。上記の解釈に従うと、 \(|\psi (x,t)|^2\)は波の振幅の二乗なので、その近辺に粒子が存在している確率が高いというわけです。
図1では波動関数\(\psi (x,0)\)の実部を図示していますが、絶対値の二乗\(|\psi (x,0)|^2\)を図示すると以下のようになります。
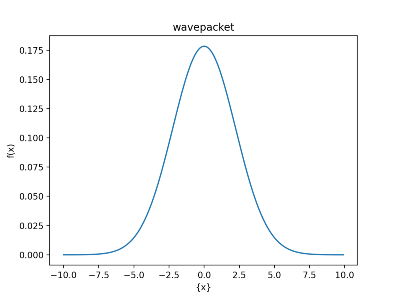
波が高くなっている\(x=0\)の辺りに粒子が存在している確率が高く、\(x=0\)から離れるにつれて 存在確率が低くなっていきます。
確率密度というのは電荷密度などと同様に、空間積分すると確率になるものです。 電荷密度と同じく\(\rho(x,t)\)という文字を使ってよく \begin{eqnarray} \rho(x,t) = |\psi (x,t)|^2 \end{eqnarray} と表します。 なぜこのような考え方をするかというと、 一般に、\(x=a\)という一点に粒子が存在する確率はほぼ\(0\)だからです。実際、(\ref{probability})式 で\(\Delta x \to 0\)の極限を取ると、 \begin{eqnarray} \int^{a+\Delta x}_{a} |\psi (x,t)|^2 dx \to 0 \end{eqnarray} になってしまうことが分かります。また、現実問題として誤差や揺らぎがあるため、 \(x=a\)という一点に粒子が存在するか議論するより、\(a \sim a+\Delta x \)の間に粒子が存在する確率 を議論した方が建設的です。
このため、確率の議論におのずと積分が必要になり、被積分関数として 確率密度が導入されます。電磁波など普通の波では、波動関数の絶対値の二乗はエネルギー密度に対応しますが、 物質波を考えるときは、確率密度と解釈されます。
規格化(レベル2)
粒子は必ず空間のどこかには存在するので、 \(-\infty \sim \infty\)の間に粒子が存在する確率は\(1\)である。 このため、確率密度の解釈を考えると、物理的な波動関数は \begin{eqnarray} \label{normal} \int^{\infty}_{-\infty} |\psi (x,t)|^2 dx = 1 \end{eqnarray} を満たす必要がある。これを波動関数の規格化条件と呼ぶ。
シュレディンガー方程式を満たす関数が全て(\ref{probability})式で物理的な解釈が可能かというと そうではありません。(\ref{normal})式を満たす\(\psi(x,t)\)のみが、物理的な意味を持ちます。
もし、あるシュレディンガー方程式の解\(\psi(x,t)\)が(\ref{normal})式を満たしていなくても、以下の手順で (\ref{normal})式を満たすものが構成できます。この操作を波動関数の規格化と呼びます。
波動関数\(\psi(x,t)\)の二乗積分は一般には\(1\)にならず、 \begin{eqnarray} \label{int} \int^{\infty}_{-\infty} |\psi (x,t)|^2 dx = |C|^2 \end{eqnarray} のようになる。(ただし、\(C\)は複素数の定数)しかし、 \begin{eqnarray} \label{normalconst} \tilde{\psi}(x,t)=\frac{1}{|C|} \psi(x,t) \end{eqnarray} と\(\tilde{\psi}(x,t)\)を定めると、これは\(\psi(x,t)\)と同じ シュレディンガー方程式を満たし、かつ規格化条件 \begin{eqnarray} \label{normal2} \int^{\infty}_{-\infty} |\tilde{\psi} (x,t)|^2 dx = 1 \end{eqnarray} を満たす。この\(\psi(x,t)\)から\(\tilde{\psi}(x,t)\)を用意する操作を 波動関数の規格化と呼ぶ。また、この時掛けた正の実数\(|C|>0\)を規格化定数と呼ぶ。
波動関数の規格化は、規格化前の関数に係数をかけることで達成されます。 具体例その1の表式に変な係数\(\frac{1}{\sqrt{10 \pi }}\)がついていたのは、この規格化条件 (\ref{normal})式を満たすためです。
通常は、上記のように正の実数\(|C|\)を掛けて規格化しますが、単純に
複素数\(C\)を掛けただけの波動関数も規格化条件を満たします。
\begin{eqnarray}
\label{normalconst2}
\tilde{\psi}_{\theta}(x,t)=\frac{1}{C} \psi(x,t)=\frac{1}{|C|e^{i \theta}} \psi(x,t)
\end{eqnarray}
(ただし、\(\theta\)は\(C\)の位相因子)
このため、(\ref{normalconst2})式のことを文脈によっては
規格化と呼んだりします。しかし、普通は慣例的に(\ref{normalconst})式のように正の実数\(|C|\)に
よって規格化します。以下、簡単に証明を置いておきます。
証明
まず、(\ref{normalconst})式によって定義された\(\tilde{\psi}(x,t)\)が規格化条件 を満たすことを確認した後、(\ref{normalconst2})式で導入した\(\tilde{\psi}_{\theta}(x,t)\) でも規格化条件を満たせることを示します。
さて、\(\int^{\infty}_{-\infty} |\psi (x,t)|^2 dx\)は 絶対値の二乗の積分なので、計算結果は必ず正の実数になる。 これを\(|C|^2\)と書くことにすれば、一般に \begin{eqnarray} \int^{\infty}_{-\infty} |\psi (x,t)|^2 dx = |C|^2 \tag{\ref{int}} \end{eqnarray} が成り立つ。(ただし、一般には\(C\)は複素数の定数。)
もし、すでに\(|C|^2=1\)なら、改めて規格化する必要はない。一方、 \(|C|^2 \neq 1\)であれば、 \begin{eqnarray} \tilde{\psi}(x,t)=\frac{1}{|C|} \psi(x,t) \end{eqnarray} と\(\tilde{\psi}(x,t)\)を定めると、 \begin{eqnarray} && \int^{\infty}_{-\infty} |\tilde{\psi} (x,t)|^2 dx \nonumber \\ &=&\frac{1}{|C|^2} \int^{\infty}_{-\infty} |\psi (x,t)|^2 dx \nonumber \\ &=& \frac{1}{|C|^2} |C|^2 \nonumber \\ &=& 1 \end{eqnarray} より、\(\tilde{\psi}(x,t)\)は規格化条件を満たす波動関数である。
つづいて\(\tilde{\psi}_{\theta}(x,t)\)についても \begin{eqnarray} &&\int^{\infty}_{-\infty} |\tilde{\psi}_{\theta} (x,t)|^2 dx \nonumber \\ &&= \left(\frac{1}{|C|e^{i \theta}}\right)^2 \int^{\infty}_{-\infty} |\psi (x,t)|^2 dx \nonumber \\ &&= \frac{1}{|C|^2} |C|^2 \nonumber \\ && = 1 \end{eqnarray} であって規格化条件(\ref{normal2})式を満たす。
さて、規格化定数\(|C|\)は正の実数なので、\(|C| =\sqrt{N}\)なる実数\(N\)が用意できて 次のように書くことも多々あります。 \begin{eqnarray} \tilde{\psi}(x,t)=\frac{1}{\sqrt{N}} \psi(x,t) \end{eqnarray}
この処方で大抵の波動関数が規格化できますが、具体例その2に挙げた平面波だけは(\ref{normal})式のような 規格化できません。その場合、少し特殊な規格化を行う必要があります。詳しくは→自由粒子
3次元の場合(レベル3)
時刻\(t\)に\((x,y,z) \sim (x+\Delta x,y+\Delta y,z+\Delta z) \)の間に粒子が存在する確率を\( P(\bs{x},t)\)とした時、 それは \begin{eqnarray} \label{probability2} P(\bs{x},t) = \int^{x+\Delta x}_{x} \int^{y+\Delta y}_{y}\int^{z+\Delta z}_{z} |\psi (\bs{x}',t)|^2 dx'^3 \end{eqnarray} で与えられる。ただし、\(\Delta x,\Delta y,\Delta z\)は十分小さいとする。
波動関数の3次元版が\(\psi(\bs{r},t)\)です。3次元になっても波動関数\(\psi(\bs{x},t)\)はベクトル関数にはならず、 スカラー関数のままなので注意してください。引数の\(\bs{x}\)のみベクトルになっています。
3次元の場合、(\ref{probability})式から(\ref{probability2})式への変更にともなって、 規格化条件は次のように修正されます。
3次元の波動関数\(\psi(\bs{x},t)\)の規格化条件は \begin{eqnarray} \int^{\infty}_{-\infty} |\psi (\bs{x},t)|^2 dx^3 = 1 \end{eqnarray} である。