光電効果
金属に光を当てると金属内部から電子が飛び出す。この現象を光電効果と呼ぶ。
高校物理でもおなじみの光電効果です。量子論の幕開けとなった重量なターニングポイントなのでしっかりおさえていきましょう。 光電効果について簡単にまとめました。
実験の内容と結果(レベル1)
光電効果の実験は以下のように行われた。
(i)ほとんど真空にしたガラス管に二枚の金属板(陽極と陰極)を挿入した。
(ii)電圧をかけ、陰極に様々な強さ、振動数の光を当てた。
(iii)電流計を使って、電流を観測した。
光電効果の実験はヘルツやレーナルト、そしてミリカンなどによって行われました。 ミリカンの実験は有名ですが、それ以前にも、光電効果はレーナルトなどによって詳しく調べられていたようです。 光電効果の実験の概略図は図1の通りで、回路を使って検証されました。
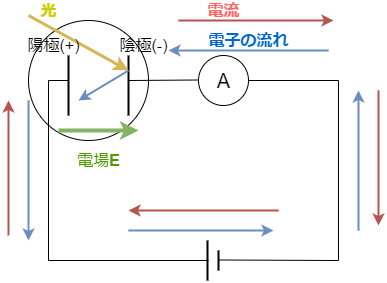
まず、ほとんど真空にしたガラス管に二枚の金属板を陽極、陰極になるように挿入します。 そして、図1のような回路を作成し、電圧をかけます。この時、光電効果以外では勝手に放電しないようにしておきます。
電圧をかけると、電子が移動し、陰極に集まってきます。反対に陽極では電子が少なくなります。 ここで陰極に対して光を当て、電子が飛び出したかを調べます。電流計によってどれだけの電子が飛び出したか 測ることが可能です。同様の実験を光の強さ、振動数を変化させて実験します。 (ミリカンは、図1を改良したような回路でより定量的な測定を行いました。)
光電効果の実験によって以下の事実が分かった。
(i)入射光の振動数\(\nu\)がある値\(\nu_{min}\)と比べて\(\nu < \nu_{min}\)なら、どれだけ強い光を当てても
電子は飛び出さない。逆にどれだけ弱い光でも、\(\nu > \nu_{min}\)なら電子は飛び出す。
(ii)強い光ほど電子は多く飛び出す。個々の電子の運動エネルギー\(T\)にはバラつきがあるが、その最大値\(T_{max}\)は
振動数に依存する。
(iii)電子は、一定のエネルギーをため込んでから飛び出すのではなく、光を当ててからすぐに飛び出す。
光電効果の実験から上述の性質が明らかになりました。ポイントは、振動数によって光電効果が起きるか起きないかが決定される
という点です。光電効果では、ある振動数\(\nu_{min}\)を超えた光を当てなければ電子は飛び出してきません。
そして、もう一つのポイントは電子が即座に飛び出してくるということです。これは電子に何か粒子が衝突していることを暗に示しています。
以下では、古典論ではこの結果が説明できないことと、光量子仮説による解釈を解説します。
ちなみにですが、陰極ではなく、陽極に光を当てても光電効果は起きません。なぜなら電子が不足している陽極には、 飛び出せる余裕のある電子がいないからです。
古典論との矛盾(レベル1)
古典論において、光は波である。また、波の強さとは即ち振幅であり、振幅の二乗を積分すると波のエネルギーになる。 つまり、光を強めると、光のエネルギーも増加する。
ここでは、先に挙げた光電効果の実験結果が古典論では説明がつかないことを見ていきます。古典論において、光は波なので
光を強めると、振動が増大し、光のエネルギーも増えるはずだと解釈されます。しかし、この解釈では光電効果は説明できません。なぜなら、
(i)光の強さを上げれば光のエネルギーが高くなるはずなので、振動数が低くても光電効果は起こるはず。
→実際にはそうなっていない。
(ii)強い光を当てれば、電子の数だけでなく、最大の運動エネルギーも増大するはず。
→そうなっていない。
(iii)光が波なら、電子にエネルギーは連続的に充填され、エネルギーが溜まってから飛び出すはず。
→そうなっていない
のように、振動数によって光電効果が起こるかどうか決まることと、電子が即座に飛び出すということが、光が波だと辻褄が合わないからです。
要は光が単純な波だと思っていると、矛盾が生まれてしまうのです。
そこで出されたのが光量子仮説でした。以下でその概略と、この仮説による鮮やかな解釈をみていきましょう。
光量子仮説による説明(レベル1)
光が振動数に比例したエネルギー \begin{equation} E = h \nu \end{equation} を持つ粒子と仮定する。この仮説を光量子仮説と呼び、この光の粒子を光子と呼ぶ。
アインシュタインが提唱した光量子仮説です。この仮説のもとで、光は \begin{eqnarray} E &=& h \nu \\ p &=& \frac{h \nu}{c} \end{eqnarray} のエネルギーと運動量を持つ粒子と解釈されます。太陽光も、蛍光灯の光も、これら光子がわんさか降ってきている のだと解釈するわけです。導出は→光量子仮説
光量子仮説において、光は粒子である。振動数をあげると、光子の一個あたりのエネルギーが増加する。 そして、光を強めると、光子の数が増える。(光子一個あたりのエネルギーは変わらない)
光量子仮説における光の解釈です。光を強めるという行為は、古典論では光のエネルギーを上げることにほかならなかったわけですが、 光量子仮説では、光子のエネルギーはそのままに、光子の数を増やす行為に対応します。結果として、全体のエネルギーは増大しますが 光子一個あたりのエネルギーは変わらないわけです。
この解釈のもとで、古典論では説明がつかなかった実験結果を考察していきます。まず、光量子仮説における光電効果とは、光子が電子に吸収され、
その分のエネルギーを受け取った電子がはじきだされる現象と理解されます。すると、
(i)高い振動数(エネルギー)を持つ光子だけが、電子をはじき出すことができる。光を強めても光子のエネルギーは変わらないため、
振動数が光電効果を起こすか決定づける。
(ii)振動数を増大させると、光子のエネルギーが増えるため、はじき出される電子の運動エネルギーも増加する。一方光を強めると、
ぶつかる光子の数が増えるので、電子の数も増える。
(iii)光は粒子なので、電子と衝突する。衝突された電子は光子を吸収した後すぐに飛び出す。
以上、光を粒子だと認めてしまえば、光電効果が自然に説明がつきました。のちにミリカンの実験によって、この解釈が正しいことが証明され、
アインシュタインはこの功績により、ノーベル賞を受賞しました。