クーロンの法則
二つの点電荷の間にはクーロン力が働く。 つまり、位置\(\bs{r}\)にある点電荷\(q\)と位置\(\bs{R}\)にある点電荷\(Q\) があるとき、電荷\(q\)が電荷\(Q\)から受ける力は \begin{equation} \label{Coulomblaw} \bs{F}_{q \gets Q}=\frac{1}{4 \pi \varep_{0}} \frac{q Q}{|\bs{r}-\bs{R}|^3} (\bs{r}-\bs{R}) \end{equation} で表せる。ここに、\(|\bs{r}-\bs{R}|\)は二つの電荷間の距離を表す。
クーロンの法則は電磁気における基本法則です。(\ref{Coulomblaw})式の別表現として、 \begin{equation} \label{Coulomblaw2} \bs{F}_{q \gets Q}=\frac{1}{4 \pi \varepsilon_{0}} \frac{q Q}{|\bs{r}-\bs{R}|^2} \bs{\hat{r}} \end{equation} があります。 ここに\(\hat{r}\)は電荷\(Q\)から電荷\(q\)に向いた方向の単位ベクトル(大きさ1のベクトル)で、 \begin{equation} \label{basisvector} \bs{\hat{r}}:= \frac{(\bs{r}-\bs{R})}{|\bs{r}-\bs{R}|} \end{equation} です。クーロンの法則について簡単にまとめました。
法則の意味(レベル1)
クーロンの法則の主張は主に
(i)二つの点電荷の間には力が働く
(ii)その力の大きさは二つの電荷の距離の2乗に反比例し、それぞれの電荷の大きさに比例する
(iii)その力の向きは同符号の電荷の場合斥力、異符号の場合引力となる
ことである。
高校物理でおなじみのクーロンの法則ですが、(\ref{Coulomblaw})式を見ると意味がつかみにくい かもしれません。しかし、(\ref{Coulomblaw2})式に書き換えるとかなり意味が見やすくなります。
\begin{equation} \bs{F}_{q \gets Q}=\frac{1}{4 \pi \varepsilon_{0}} \frac{q Q}{|\bs{r}-\bs{R}|^2} \bs{\hat{r}} \tag{\ref{Coulomblaw2}} \end{equation}まず、分母の\(qQ\)ですが、これは高校物理と同じく、クーロン力の大きさがそれぞれの電荷の大きさに比例する ことを表しています。
続いて分母の\(|\bs{r}-\bs{R}|^2\)についてですが、\(Q\)が\(\bs{R}\)に、\(q\)が\(\bs{r}\)に位置しているもとで、
ベクトル\(\bs{r}-\bs{R}\)が以下のようになるため、その大きさの二乗は\(q\)と\(Q\)の距離の2乗を表します。
(図1を参照)
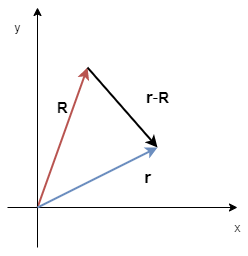
もし、\(q\)と\(Q\)が同符号の場合、\(\frac{1}{4 \pi \varepsilon_{0}} \frac{q Q}{|\bs{r}-\bs{R}|^2} \geq 0\)なので (\ref{Coulomblaw2})式より\(\bs{F}_{q \gets Q}\)は\(\bs{\hat{r}}\)と同じ向きになります。 \(Q \to q\)とは\(q\)にとって、\(Q\)から遠ざかる向きであって、これは斥力になります。
一方、\(q\)と\(Q\)が異符号の場合、\(\frac{1}{4 \pi \varepsilon_{0}} \frac{q Q}{|\bs{r}-\bs{R}|^2} \leq 0\) より\(\bs{F}_{q \gets Q}\)は\(\bs{\hat{r}}\)と逆向きになります。つまり、これは引力を表します。
基本性質(レベル1)
(\ref{Coulomblaw})式とは反対に、電荷\(Q\)が電荷\(q\)から受ける力 \(\bs{F}_{Q \gets q}\)は\(\bs{F}_{q \gets Q}\)と同じ大きさかつ逆向き。 つまり \begin{equation} \label{prop1} \bs{F}_{Q \gets q}=-\bs{F}_{q \gets Q} \end{equation} である。
クーロンの法則の基本性質の一つです。点電荷は力を受けるだけでなく、他の点電荷と 力を及ぼしあいます。そして、その向きは必ず互いに逆方向になります。これは(\ref{Coulomblaw})式 において、\(q \leftrightarrow Q\)、\(\bs{R} \leftrightarrow \bs{r}\)のように入れ替えた \begin{equation} \bs{F}_{Q \gets q}=\frac{1}{4 \pi \varep_{0}} \frac{q Q}{|\bs{R}-\bs{r}|^3} (\bs{R}-\bs{r}) \end{equation} を踏まえると確かに(\ref{prop1})式が成り立っていることが確認できます。
複数の点電荷が存在している場合、位置\(\bs{r}\)にある電荷\(q\)が 他の電荷\(q_{i} \ (i=1,2,3...n)\)から受けるクーロン力は \begin{eqnarray} & \ &\bs{F}_{q \gets \sum_{i=1}^{n} q_{i}}=\sum_{i} \bs{F}_{q \gets q_{i}}(\bs{r}) \nonumber \\ \label{Coulomblaw3} &=& \sum_{i} \frac{1}{4 \pi \varepsilon_{0}} \frac{q q_{i}}{|\bs{r}-\bs{r}_{i}|^3} (\bs{r}-\bs{r}_{i}) \end{eqnarray} のように力の和で書ける。ただし、電荷\(q_{i}\)の位置を\(\bs{r}_{i}\)と置いた。
クーロンの法則は3つ以上の電荷についても成り立ち、この場合 (\ref{Coulomblaw2})式のように単純な力の和で書けることが実験的に知られています。 このような性質を重ね合わせと呼びます。
電場による表記(レベル1)
電荷\(Q\)が位置\(\bs{r}\)に作る電場\(\bs{E}(\bs{r})\)を \(\bs{F}_{q \gets Q}=q\bs{E}(\bs{r})\)として導入する。 すると(\ref{Coulomblaw})式より \begin{equation} \bs{E}(\bs{r})=\frac{1}{4 \pi \varep_{0}} \frac{Q}{|\bs{r}-\bs{R}|^3} (\bs{r}-\bs{R}) \end{equation} である。(ただし、\(\bs{R}\)は電荷\(Q\)の位置。)
クーロンの法則(\ref{Coulomblaw})式を電場を使って書いた表式です。大学物理では基本電場を 使って色々計算します。なぜ電場を導入するのかは、場という考え方の記事を参照。
電荷が3つ以上ある場合の式(\ref{Coulomblaw3})式についても電場を用いて表すことができます。
電荷\(q_{i} \ (i=1,2,3...n)\)が位置\(\bs{r}\)に作る電場\(\bs{E}(\bs{r})\)は \begin{equation} \label{electricfield} \bs{E}(\bs{r})=\sum_{i=1}^{n} \frac{1}{4 \pi \varep_{0}} \frac{q_{i}}{|\bs{r}-\bs{r}_{i}|^3} (\bs{r}-\bs{r}_{i}) \end{equation} である。(ただし、\(\bs{r}_{i}\)は電荷\(q_{i}\)の位置。)
実際(\ref{electricfield})式に電荷\(q\)をかけると \begin{eqnarray} q \bs{E}(\bs{r})&=&\sum_{i=1}^{n} \frac{1}{4 \pi \varep_{0}} \frac{q q_{i}}{|\bs{r}-\bs{r}_{i}|^3} (\bs{r}-\bs{r}_{i}) \\ &=& \bs{F}_{q \gets \sum_{i=1}^{n} q_{i}} \end{eqnarray} となることから、確かに静電場の定義\(\bs{F}_{q \gets Q}=q\bs{E}(\bs{r})\)を満たしていることが分かります。
さらに(\ref{electricfield})式は電荷密度\(\rho(\bs{r})\)を用いると、 点電荷だけでなく、電荷が連続的に分布している場合にも適用できるように拡張することができます。 電荷密度については詳しくは→電荷密度
電荷密度\(\rho(\bs{r})\)が位置\(\bs{r}\)に作る電場\(\bs{E}(\bs{r})\)は \begin{equation} \label{electricfield2} \bs{E}(\bs{r})= \frac{1}{4 \pi \varep_{0}} \int \frac{\bs{r}-\bs{r}'}{|\bs{r}-\bs{r}'|^3} \rho(\bs{r}') dV \end{equation} である。(積分領域は全空間。)
(\ref{electricfield2})式は(\ref{electricfield})式から導出できます。
導出
(\ref{electricfield})式について、電荷\(q_{i}\)が微小な体積\(\Delta V_{i}\)を持っている と思うと、電荷密度の定義から \begin{equation} \label{chargedens} q_{i}=\lim_{\Delta V_{i} \to 0} \rho(\bs{r}_{i}) \Delta V_{i} \end{equation} とかける。点電荷が存在しない領域に対しては当然\(\rho(\bs{r}_{i})=0\)であるが、 この\(\rho(\bs{r}_{i})\)を全空間で足し上げることを考える。 即ち、(\ref{electricfield})式において\(n \to \infty\)の極限を考える。
(\ref{electricfield})式に (\ref{chargedens})式を代入して\(n \to \infty\)の極限を取ると \begin{eqnarray} & \ &\bs{E}(\bs{r}) \nonumber \\ &=& \lim_{\Delta V_{i} \to 0, n \to \infty } \sum_{i=1}^{n} \frac{1}{4 \pi \varep_{0}} \frac{(\bs{r}-\bs{r}_{i})}{|\bs{r}-\bs{r}_{i}|^3} \rho(\bs{r}_{i}) \Delta V_{i} \nonumber \\ &=& \frac{1}{4 \pi \varep_{0}} \int \frac{\bs{r}-\bs{r}'}{|\bs{r}-\bs{r}'|^3} \rho(\bs{r}') dV \end{eqnarray} となって、(\ref{electricfield2})式を得る。
(\ref{electricfield2})式は点電荷だけでなく、電荷の連続分布にも対応しているという点で、クーロンの法則の 一般化になっています。しかし、この積分は実行が面倒(または実行不可能)なことが多く、現実ではガウスの法則を用いた方が 楽になる場合が多いです。(ガウスの法則については→こちらから)
ちなみに(\ref{electricfield2})式の積分領域は全空間なので、デカルト座標で書くと次のようになります。
(\ref{electricfield2})式はデカルト座標で積分を書くと \begin{equation} \bs{E}(\bs{r})= \frac{1}{4 \pi \varep_{0}} \int_{-\infty}^{\infty} \frac{\bs{r}-\bs{r}'}{|\bs{r}-\bs{r}'|^3} \rho(\bs{r}') dxdydz \end{equation} である。(積分領域は\(x,y,z\)それぞれで\(-\infty ~ \infty\))
物理では積分領域が全空間(\(-\infty ~ \infty\))の場合、基本的に積分範囲を省略して書きます。 また、この表記から分かるように、この積分が実行できるのは全空間(全宇宙)にわたって電荷密度\(\rho(\bs{r})\) の値が分かっている場合のみです。なので、上でも述べたように、(試験問題ならともかく)現実の問題ではこの積分は基本的に実行不可能です。