ベクトル/スカラーの座標変換
座標変換に対し、ベクトルは成分が変化するが、スカラーは変化しない
ベクトルとスカラーが持つ重要な性質の一つに、座標変換に対する変換性があげられます。 ベクトル/スカラーと座標変換の関係性について、要点をまとめました。
具体例(レベル1)
(i)2次元座標における回転
座標軸を\(\theta\)だけ回転させる変換について、 ベクトルは \begin{equation} \left (\begin{array}{c} x \\ y \end{array} \right) \to \left (\begin{array}{c} x' \\ y' \end{array} \right) \end{equation} ただし、 \begin{equation} \label{rotate} \left (\begin{array}{c} x' \\ y' \end{array} \right) = \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta& \cos \theta \end{pmatrix} \left (\begin{array}{c} x \\ y \end{array} \right) \end{equation} のように成分が変化しますが、スカラー(内積)は回転変換のもとで \begin{equation} x'^2+y'^2=x^2+y^2 \end{equation} のように不変です。座標の回転について詳しくは→座標の回転
(ii)極座標変換
極座標への基底のとりかえにより、 ベクトルは \begin{equation} \left (\begin{array}{c} x \\ y \end{array} \right) \to \left (\begin{array}{c} r \\ 0 \end{array} \right) \end{equation} ただし \begin{equation} \label{polar} \left (\begin{array}{c} r \\ 0 \end{array} \right) = \begin{pmatrix} \cos \theta & \sin \theta \\ -\sin \theta& \cos \theta \end{pmatrix} \left (\begin{array}{c} x \\ y \end{array} \right) \end{equation} のように成分が変化しますが、スカラー(内積)は \begin{equation} x^2+y^2=r^2 \end{equation} なので値は変わりません。 極座標表示についいて詳しくは→ベクトルの極座標表示
ここでは位置ベクトルの成分と大きさを例に挙げていますが、他のベクトル(速度、加速度など)についても 同じことがいえます。
変換公式(レベル2)
座標変換に対し、位置ベクトルの成分\(x_{i}\)は行列\(R_{ij}\) より \begin{equation} \label{trans} x'_{i}=\sum_{j} R_{ij} x_{j} \end{equation} と変換されるが、他のベクトル(速度、加速度など)も (\ref{trans})式に則って変換される。(ただし例外あり)
また、スカラーに関しては座標変換に対し、 \begin{equation} |\bs{x}'|= |\bs{x}| \end{equation} のように不変である。
上の具体例からも分かる通り、ベクトルの成分の 座標変換は行列によって表すことができます。2次元ならば、\(2 \times 2\)行列、 3次元ならば、\(3 \times 3\)行列で変換されるといった具合です。
ただし、例外として、平行移動は(\ref{trans})式では書けません。 また、座標変換が時間に依存する場合、必ずしも変換は(\ref{trans})式で書けるとは限りません。
ここでは、位置ベクトルの変換が(\ref{trans})式に従う時、他のベクトルの変換も (\ref{trans})式に従うことを示します。
証明
力学で出てくるベクトルは位置\(\bs{x}\)、 速度\(\bs{v}\)、加速度\(\bs{a}\)、力\(\bs{F}\)しかないので これらが同じ変換則(\ref{trans})式に従うことを示せばいいわけです。
(\ref{trans})式を両辺時間で微分すると、 \begin{equation} \dot{x}'_{i}=\sum_{j} R_{ij} \dot{x}_{j} \end{equation} より、速度\(\bs{v}=\dot{\bs{x}}\)の変換は (\ref{trans})式に従う。さらに微分すると同様に 加速度\(\bs{a}=\ddot{\bs{x}}\)も(\ref{trans})式に従うと分かる。
最後に、運動方程式\(m \ddot{\bs{x}} =\bs{F}\)が正しいとするならば、 右辺の力\(\bs{F}\)も(\ref{trans})式に従うと分かる。
ベクトルそのものの変換(レベル2)
ベクトルの成分は座標変換で変化するが、ベクトルそのものは 座標変換で変化しない。
つまり、あるベクトル\(\overrightarrow{OP}\)について、 座標系の回転前と回転後を比べると \begin{equation} \overrightarrow{OP}_{回転前}=\overrightarrow{OP}_{回転後}\ \end{equation} が成り立つ。(ただし成分表示は変化する。)
今まで、ベクトルの成分表示が座標変換に対して変化することを見てきましたが、 実はベクトルそのものは座標変換に対し、不変です。
例として、以下の二つの図を見比べてみましょう。
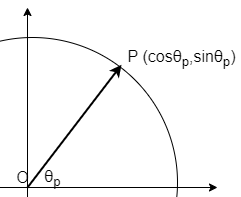
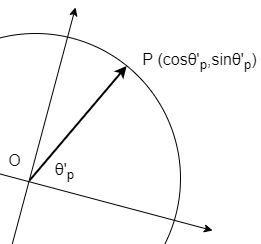
上の図には単位円上にとった\(P\)と\(O\)を結ぶベクトル\(\overrightarrow{OP}\)が書かれています。
座標の回転により、線分\(OP\)と\(x\)軸となす角度が\(\theta_{p}\)から\(\theta'_{p}\)へ変化したため、 成分表示は確かに変化しています。しかしながら、ベクトル\(\overrightarrow{OP}\) について、図1と図2の矢印は平行で、向きも大きさも変化していません。 つまり、ベクトルの定義から両者は等しく、 座標変換の前後でベクトルそのものは変化していないということです。
この事実は、成分表示ではなく、基底表示を用いると分かりやすくなります。 回転前と後の\(\overrightarrow{OP}\)について、それぞれ基底表示で書いてみます。 基底表示について詳しくはこちらからどうぞ。 \begin{equation} \label{vector1} \overrightarrow{OP}_{回転前}=\cos \theta_{p} \bs{e}_{x} +\sin \theta_{p} \bs{e}_{y} \end{equation} \begin{equation} \label{vector2} \overrightarrow{OP}_{回転後}=\cos \theta'_{p} \bs{e}_{x'} +\sin \theta'_{p} \bs{e}_{y'} \end{equation} (回転により、基底も変化していることに注意) 実は成分の変換は、基底の変換によって相殺されます。つまり、 \(\overrightarrow{OP}_{回転前}=\overrightarrow{OP}_{回転後}\)が成り立ちます。
このことを計算によって確かめてみましょう。計算
途中、ベクトルの座標軸回転の公式(\ref{rotate})を 使います。詳しくは→座標の回転
右辺が一致することを示す。まず \begin{equation} (\ref{vector2}の右辺) = (\bs{e}_{x'} , \bs{e}_{y'} ) \left (\begin{array}{c} \cos \theta'_{p} \\ \sin \theta'_{p} \end{array} \right) \end{equation} であるが、\(\theta'_{p}=\theta_{p}+\theta\)として \begin{equation} \left (\begin{array}{c} \cos \theta_{p}' \\ \sin \theta'_{p} \end{array} \right) = \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta& \cos \theta \end{pmatrix} \left (\begin{array}{c} \cos \theta_{p} \\ \sin \theta_{p} \end{array} \right) \end{equation} が成り立つ。基底ベクトルについても同様の公式が成り立つが、 計算に使うのはこれの転置をとったもの \begin{equation} (\bs{e}_{x'} , \bs{e}_{y'} ) =(\bs{e}_{x} , \bs{e}_{y} ) \begin{pmatrix} \cos \theta & \sin \theta \\ -\sin \theta& \cos \theta \end{pmatrix} \end{equation} である。この二つを代入すると \begin{equation} (\bs{e}_{x'} , \bs{e}_{y'} ) \left (\begin{array}{c} \cos \theta'_{p} \\ \sin \theta'_{p} \end{array} \right) = (\bs{e}_{x} , \bs{e}_{y} ) \left (\begin{array}{c} \cos \theta_{p} \\ \sin \theta_{p} \end{array} \right) \end{equation} が確認できる。以上から、(\ref{vector2})の右辺と (\ref{vector1})の右辺が等しいことが示せた。