ケプラーの第1法則
惑星の軌道は太陽を1焦点とする楕円である。
惑星の軌道に関して強い主張を与えるのがこの第1法則です。図で表すと、太陽と 惑星の位置関係が次のようになっているということです。
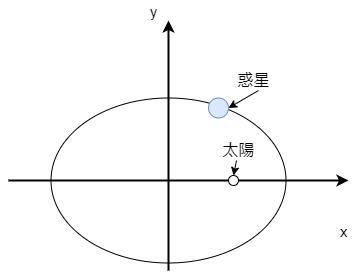
図では少し大げさに書いています。実際の軌道はかなり真円に近いです。
このことについてはこちらから
導出(レベル1)
ケプラーの法則は全て万有引力から導出できます。 計算に入る前に導出の指針を示しておきます。
軌道が楕円であることを示すには\(r\)と\(\theta\)の間に \begin{equation} \label{ellipse} r=\frac{l}{1+e \cos \theta} \end{equation} が成り立つことを示せればよい。(ただし、\(l,e\)は定数で、 \(0 \leq e < 1\))
軌道を求めるだけならば、運動方程式を完全に解く必要はありません。 (\ref{ellipse})式を導出する方が楽に示せます。 (\ref{ellipse})式が楕円を表しているかギモンな人は二次曲線の極座標表示 を参照してください。
では、この指針に従って、運動方程式から軌道が楕円になることを 導きます。少し長くなるので、二つに区切って方針を整理します。
導出
まず、運動方程式の極座標表示は \begin{eqnarray} \label{EOM1} &m& (\ddot{r} - r \dot{\theta}^2)=-G\frac{Mm}{r^2} \\ \label{EOM2} &m& \frac{1}{r} \frac{d}{d t}(r^2 \dot{\theta} )=0 \end{eqnarray} であるが、(\ref{EOM1})から、\(t\)微分を消去して、\(\theta\)微分 などに書き換えることを目指す。 ((\ref{ellipse})式の右辺には\(\theta\)しか変数がでてこないため)
さて、(\ref{EOM2})式より \begin{equation} r^2 \dot{\theta}=(定数) \end{equation} なので、この定数を\(h\)と置くと \begin{equation} \dot{\theta}=\frac{h}{r^2} \end{equation} となって、\(\theta\)の\(t\)微分 は\(r\)で書き換えることができると分かった。
また、合成関数の微分の公式より、\(r\)の\(t\)微分についても \begin{equation} \frac{d r}{dt}=\frac{d \theta}{dt} \frac{d r}{d \theta} = \dot{\theta} \frac{d r}{d \theta} \end{equation} と変形でき、\(h\)を使って\(\dot{\theta}\)を消すと \begin{equation} \dot{r}=\frac{h}{r^3}\frac{d r}{d \theta} \end{equation} を得る。\(\ddot{r}\)についても同様に \begin{eqnarray} \ddot{r}&=&\frac{d}{dt} \dot{r} \\ &=&\frac{d \theta}{dt} \frac{d }{d \theta} \dot{r} \nonumber \\ &=&\dot{\theta} \frac{d }{d \theta} \left( \frac{h}{r^3}\frac{d r}{d \theta} \right) \nonumber \\ &=&\frac{h}{r^2}\frac{d }{d \theta} \left( \frac{h}{r^3}\frac{d r}{d \theta}) \right) \end{eqnarray} を得る。
以上より、(\ref{EOM1})から、\(t\)微分を全て消去でき、 得られるのは\(r\)の\(\theta\)に関する微分方程式 \begin{equation} \frac{h}{r^2} \frac{d }{d \theta} \left( \frac{h}{r^3}\frac{d r}{d \theta} \right) - \frac{h^2}{r^3} =-G\frac{M}{r^2} \end{equation} が得られた。両辺に\(\frac{r^2}{h^2}\)を掛けておくと \begin{equation} \label{diffeq} \frac{d }{d \theta} \left( \frac{1}{r^3}\frac{d r}{d \theta}\right) - \frac{1}{r} =-G\frac{M}{h^2} \end{equation} のようにもかける。
あとは、(\ref{diffeq})式を解いて、解が(\ref{ellipse})式であることを確認すればいい。 分数\(\frac{1}{r}\)を含む微分方程式の定石として、\(r\)をかけて分母を払うか、または \begin{equation} u=\frac{1}{r} \end{equation} のように置いてしまって、\(u\)の微分方程式に帰着するという方法がある。今回は 後者を使って\(u\)の微分方程式に帰着する。
まず、先に\(u\)の微分を計算しておこう。再び合成関数の微分公式より、 \begin{equation} \frac{d u}{d \theta} =\frac{d u}{dr} \frac{d r}{d \theta} =-\frac{1}{r^2} \frac{d r}{d \theta} \end{equation} なので、 \begin{equation} \frac{d r}{d \theta} = -r^2 \frac{d u}{d \theta} \end{equation} が成り立つ。これを(\ref{diffeq})式に代入すると、 \begin{equation} \frac{d^2 u}{d \theta^2} + u=G\frac{M}{h^2} \end{equation} となる。すると、この微分方程式は 単振動の微分方程式 になっている。
なぜなら、\(G\frac{M}{h^2}=\frac{1}{l}\)とおいて、 \begin{equation} \frac{d^2 (u-\frac{1}{l})}{d \theta^2} =-(u-\frac{1}{l}) \end{equation} のようにして(\(\frac{1}{l}\)は定数なので、\(\frac{d^2 (u-\frac{1}{l})}{d \theta^2}=\frac{d^2 u}{d \theta^2}\)なことに 注意。) \(u-\frac{1}{l}=x\)とでもおいてやると、 \begin{equation} \frac{d^2 x}{d \theta^2}=-x \end{equation} のように変形できるからである。
さて、この単振動型の微分方程式の一般解は三角関数を使うと \begin{equation} x=A\cos (\theta+\alpha) \end{equation} となる。ただし、\(A\)と\(\alpha\)は定数。 あとは、\(u-\frac{1}{l}=x\)を代入すれば、 \begin{equation} u(\theta)=A\cos (\theta+\alpha) +\frac{1}{l} \end{equation} となって、さらに\(u=\frac{1}{r}\)をだったから \begin{equation} r=\frac{1}{A\cos (\theta+\alpha) +\frac{1}{l}} \end{equation} を得る。最後に\(\alpha=0\)を代入して、\(A=\frac{e}{l}\)とおく。 以上により \begin{equation} r=\frac{l}{1+e \cos \theta} \tag{\ref{ellipse}} \end{equation} が導けた。
以上により、万有引力に従う物体の運動の軌跡が(\ref{ellipse})式 で表せることが示せました。楕円であることを言うためには、 更に\(0 \leq e < 1\)であることを示す必要があります。 詳しくは次のギモン参照。
軌道の分類(レベル1)
以下の式 \begin{equation} r=\frac{l}{1+e \cos \theta} \tag{\ref{ellipse}} \end{equation} が表す軌道は離心率\(e\)により4種類に分類できる。 \begin{eqnarray} 円:&e&=0 \nonumber \\ 楕円:&0& < e < 1 \nonumber \\ 放物線:&e&=1 \nonumber \\ 双曲線:&e& > 1 \nonumber \end{eqnarray}
(\ref{ellipse})式で表せる軌道を二次曲線といいますが、
離心率\(e\)に
よって、どの二次曲線を表すのか変わります。
詳しくは→二次曲線の極座標表示
実は、今回の場合、離心率が物体のエネルギーに依存しており、離心率で 分類する代わりに、エネルギーで軌道を判別することができます。
万有引力のもとで、軌道の離心率とエネルギーの間には関係式 \begin{equation} \label{Eande} E=mh^2 \frac{e^2-1}{2l^2} \end{equation} が成り立つ。特に、軌道が円(\(e=0\))の時、 \begin{equation} E= -\frac{mh^2}{2l^2} \end{equation} である。
導出
ここでは(\ref{Eande})式を導出します。使うのは(\ref{ellipse})式 とその導出の過程で置いた\(G\frac{M}{h^2}=\frac{1}{l}\) 及び、万有引力の力学的エネルギーの表式 \begin{equation} \label{energy} E=\frac{1}{2}m\boldsymbol{v}^2 - \frac{GMm}{r} \end{equation} です。
まず、速度を極座標表示すると、 \begin{equation} \frac{d \boldsymbol{r}}{dt} = \dot{r} \boldsymbol{e}_{r} + r \dot{\theta} \boldsymbol{e}_{\theta} \tag{24} \end{equation} となるので、これを使って、(\ref{energy})式を \begin{equation} E=\frac{1}{2}m(\dot{r}^2+(r \dot{\theta})^2) - \frac{GMm}{r} \tag{23} \end{equation} と変形する。これは\(h=r^2 \dot{\theta}\)なる\(h\) を使えば\(r\)だけを使って \begin{equation} \label{energy2} E=\frac{1}{2}m(\dot{r}^2+\frac{h^2}{r^2}) - \frac{GMm}{r} \tag{24} \end{equation} のようにも表せる。ここに(\ref{ellipse})式を代入すれば、\(E\)と\(e\) の関係式を出すことができる。
代入の前に、少し条件を入れて計算をしやすくしておく。 (\ref{ellipse})式において\(r\)は\(\theta=0\)の時、最小値 \begin{equation} \label{ellipse2} r=\frac{l}{1+e} \end{equation} を取る。\(r\)が最小値を取るということは、 この時\(\dot{r}=0\)である。よって、\(E\)の式は\(\theta=0\)の時 \begin{equation} \label{energy3} E=\frac{1}{2}m\frac{h^2}{r^2} - \frac{GMm}{r} \end{equation} である。
最後に(\ref{energy3})式に(\ref{ellipse2})式を代入する。結果は \begin{equation} \frac{1}{2}\frac{h^2(1+e)^2}{l^2}-\frac{GM(1+e)}{l}=\frac{E}{m} \end{equation} のようになる。ここで両辺を\(h^2\)で割って\(G\frac{M}{h^2}=\frac{1}{l}\) を使うと、 \begin{equation} \frac{1}{2}\frac{(1+e)^2}{l^2}-\frac{1+e}{l^2}=\frac{E}{mh^2} \end{equation} まで変形できる。更にこの式を整理すると \begin{equation} E=mh^2 \frac{e^2-1}{2l^2} \tag{\ref{Eande}} \end{equation} を得る。
この関係式により、楕円の条件(\(0 \leq e < 1\))を\(E\)の条件として \begin{equation} -\frac{mh^2}{2l^2} < E <0 \end{equation} と書き換えることができます。
エネルギーが負になっていて気持ち悪いですが、これについては問題なくて、 なぜなら(\ref{energy})式において、無限遠方\(r \to \infty\)を考えると、 \begin{equation} E=\frac{1}{2}m\boldsymbol{v}^2 \end{equation} となって、仮に\(E > 0\)なら無限遠でも運動エネルギーを持ってしまうからです。 つまり、\(E < 0\)でないと無限遠まで飛んで行ってしまって 軌道が楕円には絶対にならないということです。
逆に、惑星が無限遠へ飛んでいかないということは\(E < 0\)が満たされている ので惑星の軌道が楕円か円になることが分かります。
最後に、以上の結果をまとめておきます。
以下の式 \begin{equation} r=\frac{l}{1+e \cos \theta} \tag{\ref{ellipse}} \end{equation} が表す軌道は離心率\(e\)により4種類に分類できる。 \begin{eqnarray} 円:&e&=0 \to E= -\frac{mh^2}{2l^2}\nonumber \\ 楕円:&0& < e < 1 \to -\frac{mh^2}{2l^2} < E < 0 \nonumber \\ 放物線:&e&=1 \to E=0 \nonumber \\ 双曲線:&e& > 1 \to E>0 \nonumber \end{eqnarray} ただし、\(E\)は力学的エネルギー。