ガウスの定理

証明

まずは式(\ref{Gausstheorem})が微小な直方体に対して成り立つことを示す。そのために、 微小な体積\( \Delta V=\Delta x \Delta y \Delta z\)を持つ下図のような直方体を考える。 これがベクトル場\(\bs{E}(\bs{r})\)の中にあるとする。

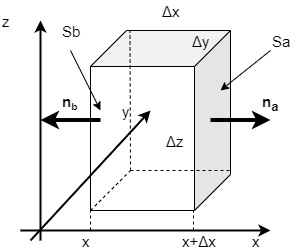
はじめに、\(x\)軸に垂直な二つの面を考える。これらを\(x\)座標が大きい方から面\(S_{a}\)、面\(S_{b}\)と呼ぶことにする。 それぞれの面における法線ベクトルは成分をかくと、図のように\(\bs{n}_{a}=(1,0,0)\)、\(\bs{n}_{b}=(-1,0,0)\)である。

面\(S_{b}\)の\(x\)座標を「\(x\)」とすると、面\(S_{a}\)の\(x\)座標は「\(x+\Delta x\)」になるので、 この二つの面上において、垂直成分の\(\bs{E}(\bs{r})\)の積分の和は \begin{eqnarray} & \ &\int_{S_{a}} \bs{E} \cdot \bs{n}_{a} \mathrm dS +\int_{S_{b}} \bs{E} \cdot \bs{n}_{b} \mathrm dS \nonumber \\ &=&\int_{S_{a}} E_{x}(x+\D x,y,z) dydz \nonumber \\ &\qquad &-\int_{S_{b}} E_{x}(x,y,z) dydz \end{eqnarray} になる。

ここで、\(E_{x}(x,y,z)\)は定数ではないが、十分積分領域が微小ならば 平均して面のど真ん中の値、\(E_{x}(x,y+\frac{\Delta y}{2},z+\frac{\Delta z}{2})\)で一定値をとるものとして近似し、積分の外へ 出すことができる。(厳密にはテイラー展開する必要があります→積分中のテイラー展開)
\(E_{x}(x+\D x,y,z)\)にも同様の近似を施すと、 \begin{eqnarray} & \ &\int_{S_{a}} E_{x}(x+\D x,y,z) dydz \nonumber \\ &\qquad& -\int_{S_{b}} E_{x}(x,y,z) dydz \nonumber \\ &=&E_{x}(x+\Delta x,y+\harfD{y},z) \int_{S_{a}} dydz \nonumber \\ &\qquad& -E_{x}(x,y+\harfD{y},z) \int_{S_{b}} dydz \nonumber \\ &=& \left[ E_{x}(x+\D x,y+\harfD{y},z+\harfD{z}) \right. \nonumber \\ &\qquad& \left. -E_{x}(x,y+\harfD{y},z+\harfD{z}) \right] \Delta y \Delta z \\ \end{eqnarray} のように積分を実行できる。

あとは、少し変形してあげると \begin{eqnarray} &=&\frac{1}{\D x} \left[E_{x}(x+\D x,y+\harfD{y},z+\harfD{z})\right. \nonumber \\ & \ & \left.-E_{x}(x,y+\harfD{y},z+\harfD{z}) \right] \D x \D y \D z \nonumber \\ & \ & \tolim{\D x}{0} \pdiff{E_{x}}{x}(x,y+\harfD{y},z+\harfD{z})\Delta V \nonumber \\ & \ & \tolim{\D y \D z}{0} \pdiff{E_{x}}{x}(x,y,z)\Delta V \end{eqnarray} をえる。

さて、他の\(y\)軸、\(z\)軸に垂直な二つの面のペアでそれぞれ同じ計算をすると、面積分はそれぞれ \(\pdiff{E_{y}}{y}(x,y,z)\Delta V,\pdiff{E_{z}}{z}(x,y,z)\Delta V\) になるので、この直方体全体では \begin{eqnarray} & \ &\int_{\partial (\Delta V)}\bs{E} \cdot \bs{n} \mathrm dS \nonumber \\ &=&(\pdiff{E_{x}}{x}+\pdiff{E_{y}}{y}+\pdiff{E_{z}}{z})\Delta V \nonumber\\ &=&\int_{\Delta V} \nabla \cdot \bs{E}(\bs{r}) \mathrm dV \end{eqnarray} となって、式(\ref{Gausstheorem})が示せた。(ここに、\(\partial (\Delta V)\)は\(\D V\)の表面を表す。)

最後に、微小ではない、任意の形状の領域\(V\)で式(\ref{Gausstheorem})が成り立つことを示す。

まず、どんな形状の領域であっても、その領域を微小な直方体に分割して近似することは可能である。 また、微小な各直方体に関しては式(\ref{Gausstheorem})が成り立つことが分かっているので、 全ての直方体について式(\ref{Gausstheorem})の和をとると、 \begin{eqnarray} \label{rectangularsum} &\sum_{i}\int_{\Delta V_{i}} \nabla \cdot \bs{E}(\bs{r}) \mathrm dV \nonumber \\ &=\sum_{i} \int_{\partial (\Delta V_{i})}\bs{E} \cdot \bs{n}(\bs{r}) \mathrm dS \end{eqnarray} さて、限りなく微小な直方体で領域を近似していくと、左辺の値は式(\ref{Gausstheorem})の左辺に一致する。 一方、右辺については、隣り合う面上では\(\bs{E}(\bs{r})\)の値は等しいかつ、向きが反対のため 積分が互いに打ち消しあう。 その結果、隣り合う面のない、\(S\)の表面のみ積分の値が残り、これは式(\ref{Gausstheorem})の右辺に一致する。 こうして、任意の領域でも式(\ref{Gausstheorem})が成り立つことが示せた。

解説

ここでは厳密な証明ではなく、ざっくりとした説明を与えます。

まず、ある領域を近似的に構成するために、直方体のブロックを\(N^3\)個程度使ったする。 (イメージとしては、縦と横がそれぞれ\(N\)個くらい、高さも\(N\)個くらいブロックを使ったということ) 以下、この近似をブロック近似と呼ぶことにする。

一つ一つの直方体ブロックが大きい時、つまり近似が粗い時、表面は凸凹したものになる。 よって、当然対象の領域が丸みを帯びていると、計算結果に誤差が生じる。 しかしながら、その差は表面で生まれるため、生じる誤差は領域の表面積に比例し、 ブロック数で表すと、\(O(N^2)\)である。

参考：例えば、球の体積について、一皮大きく近似された直方体ブロックの集合体と、一皮小さく近似されたもの の差は \begin{equation} \frac{4}{3}\pi (N+1)^3- \frac{4}{3}N^3 \simeq 4 \pi N^2 \end{equation} のように\(O(N^2)\)である。つまり、実際の球の体積と、ブロック近似された球の誤差は 高々(大体)\(O(N^2)\)。

ゆえに、全体に対する、誤差の割合は \begin{equation} \frac{O(N^2)}{O(N^3)} \tolim{N}{\infty} 0 \end{equation} となるため、ブロックの大きさを小さくして使用数\(N^3\)を増やすと、 つまり近似の精度を上げていくと、誤差の部分は無視できるほど小さくなるということが分かる。