ベクトルの発散
ベクトル\(\bs{V}(\bs{r})\)に対し、 \begin{equation} \nabla \cdot \bs{V}(\bs{r})=\pdiff{V_{x}}{x}(\bs{r})+\pdiff{V_{y}}{y}(\bs{r})+\pdiff{V_{z}}{z}(\bs{r}) \end{equation} をベクトル\(\bs{V}(\bs{r})\)の発散と呼ぶ。
ベクトルの発散は特に電磁気学で多用されます。物理的な意味までよく理解しましょう。 \(\nabla \cdot \nabla \times \bs{V}=0\)など\(\nabla\)に関する公式についてはナブラの公式(基本編)も あわせてどうぞ
発散のことを\(\mathrm{div}\)を使って、\(\nabla \cdot \bs{V}=\mathrm{div} \bs{V}\) とも表したりもしますが、両者は同じ意味です。
具体例(レベル1)
具体例を通して直感を養いましょう。
具体例その1
\(a\)を定数として\(V(\bs{r})=a \bs{r}\)を考える。これの発散は \begin{equation} \nabla \cdot (a \bs{r})= a \end{equation} である。
後述するように、発散はベクトルの湧き出し(吸い込み)を表します。実際 \(a \bs{r}\)は図示すると、\(a > 0\)ならベクトルが外向きに出ていて、原点からベクトルが湧き出しているように見えます。 \(a < 0\)だと、ベクトルの向きが反転し、 吸い込みになります。
発散は微分なので、定数ベクトル\(V(\bs{r})=\bs{c}\)に対し \(\nabla \cdot \bs{c}=0\)です。これは定数ベクトルを図示しても、(湧き出しのない)ただの流れにしか 見えないことに対応しています。
ちなみに、発散の値が大きいほど、湧き出し(吸い込み)が強いと解釈されます。
具体例その2
等速円運動の速度ベクトル \begin{eqnarray} \bs{v}(\bs{r})=\left( \begin{array}{c} -\omega y \\ \omega x \\ 0 \\ \end{array} \right) \end{eqnarray} の発散を考える。計算するとこれは\(0\)になる。 \begin{equation} \nabla \bs{v}(\bs{r})= 0 \end{equation} つまり、質点の回転に対応するベクトルに発散はない。
速度ベクトル\(\bs{v} = r \omega \bs{e}_{\theta}\)の発散は\(0\)です。 円運動のベクトルを図示しても、湧き出しのような構造は見られないため、物理的な直感と合致しています。 回転に対応するベクトルは発散は\(0\)ですが、ベクトルの回転を考えると値を返します。 詳しくは→ベクトルの回転
発散の意味(レベル1)
発散とは単位体積あたりのベクトルの湧き出し(吸い込み)のことである。
上記の湧き出しとは言葉通り、温泉のようににその点から何かが湧き出していることを表します。 湧き出しか吸い込みかは、発散の符号で判定します。 なぜそうなるのかを図を使って解説していきましょう。
解説
まず、体積\( \Delta V=\Delta x \Delta y \Delta z\)を持つ微小な直方体を考えます。この直方体はベクトル\(\bs{V}(\bs{r})\)の流れの中にあるとします。 イメージ的には、例えば川のような水の流れの中に小さな仮想の直方体を考える感じです。(体積の\(\Delta V\)とベクトルの\(\bs{V}\) を混同しないよう注意してください。)
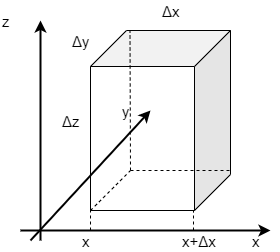
直方体の面のうち、\(x\)軸に垂直な二つの面に注目します。まず、上流側の面の\(x\)座標を「\(x\)」とおくと、
この面の面積は\(\Delta y \Delta z\)なので、この面を通じて入ってくる流れの量は\(V_{x}(x,y,z)\Delta y \Delta z\)になります。
一方、下流側の面の\(x\)座標は「\(x+\Delta x\)」なので、この面から出ていく流れは、\(V_{x}(x+\Delta x,y,z)\Delta y \Delta z\)になります。
よって、この二つの面の流れの差を取ることで、実質出ていく(つまり湧き出す)量は \begin{eqnarray} & \ &\{V_{x}(x+\Delta x,y,z)-V_{x}(x,y,z)\} \Delta y \Delta z \nonumber \\ &=&\frac{V_{x}(x+\Delta x,y,z)-V_{x}(x,y,z)}{\Delta x}\Delta x \Delta y \Delta z \nonumber \\ & \ & \underset{{\Delta x,\Delta y,\Delta z \to 0}}{\longrightarrow} \pdiff{V_{x}}{x} \Delta V \end{eqnarray} と求めることができます。
同じことを\(y\)軸、\(z\)軸に垂直な二つの面のペアで行います。その全てを合算することで、この直方体から湧き出る流出量の総和を 求めることが可能です。その結果は \begin{eqnarray} & &\left( \pdiff{V_{x}}{x}(\bs{r})+\pdiff{V_{y}}{y}(\bs{r})+\pdiff{V_{z}}{z}(\bs{r}) \right) \Delta V \nonumber \\ &=& \nabla \cdot \bs{V}(\bs{r}) \mathrm \Delta V \end{eqnarray} のように発散に\(\Delta V\)を掛けたものになっているため、確かに発散を湧き出しと捉えられることが分かりました。
ちなみに、以上の議論は流れの向きが逆の場合でも、つまり、上流と下流が逆でも同じ式が成り立ち、場合分けは不要です。 なぜなら、負の流れの流入は正の流れが出ていくこととみなせるからですね。(逆も同様)
極座標の表示(レベル2)
発散は三次元の極座標(球面座標)において、以下で表される。 \begin{equation} \label{3polor} \nabla \cdot \bs{V}(\bs{r})=\frac{1}{r^2}\pdiff{}{r}(r^2 V_{r})+\frac{1}{r \sin \theta}\pdiff{}{\theta} (\sin \theta V_{\theta}) +\frac{1}{r \sin \theta} \pdiff{}{\phi} V_{\phi} \end{equation} (ただし、\(r \neq 0\)とする)
発散の極座標表示です。 \begin{equation} \nabla \cdot \bs{V}(\bs{r})=\pdiff{V_{r}}{r}+\pdiff{V_{\theta}}{\theta}+\pdiff{V_{\phi}}{\phi} \end{equation} のように綺麗な表式にならないのは、極座標の基底ベクトル\(\bs{e}_{r},\bs{e}_{\theta},\bs{e}_{\phi}\)も 微分されるので、その寄与が入るからです。
(\ref{3polor})式について、\(\bs{V}\)が動径成分しか持たず、\(\bs{V}(\bs{r})=|\bs{V}(\bs{r})| \bs{e}_{r}\)と 書けるとき、 \begin{equation} \label{rdiv} \nabla \cdot \bs{V}(r)=\frac{1}{r^2}\pdiff{}{r}(r^2 V_{r}) \end{equation} (ただし、\(r \neq 0\) ,\(\bs{e}_{r}\)は\(\hat{\bs{r}}\)と表記することもある)
クーロン力などの中心力は\(\bs{F} = \frac{A}{4 \pi r^2} \bs{e}_{r}\)の形をしているので、この公式が使えます。 愚直に(\ref{rdiv})代入すると\(r \neq 0\)において \begin{equation} \label{centralforce} \nabla \cdot \bs{F}(\bs{r})=0 \end{equation} を得られます。
ところが、これは一見直感と反しています。なぜなら、クーロン力は図示すると、中心から湧き出し(吸い込み)が見えるはず だからです。これは(\ref{rdiv})式が が\(r=0\)で定義されていないためで、真面目に\(r=0\)の寄与まで入れると \begin{equation} \nabla \cdot \bs{F}(\bs{r})=A \delta(r) \end{equation} になり、直感通り\(r=0\)で湧き出しが発散します。
この式の導出は中心力とポテンシャルの関係式 \(\bs{F} = -\nabla \frac{A}{4 \pi r}\) の両辺の発散を取り、デルタ関数の公式 \begin{equation} \nabla^2 \frac{1}{4 \pi r}=-\delta(r) \end{equation} を使うと導けます。
勾配と発散の違い(レベル1)
\(\nabla\)を掛けるものには発散「\(\nabla \cdot \bs{V}\)」以外に勾配「\(\nabla f\)」があります。 両者は似ていますが、定義を見ると違いは一目瞭然です。
スカラー関数\(f(\bs{r})\)に対し、 \begin{equation} \nabla f(\bs{r})=\left (\begin{array}{c} \pdiff{f}{x}(\bs{r}) \\ \pdiff{f}{y}(\bs{r})\\ \pdiff{f}{z}(\bs{r}) \end{array} \right) \end{equation} をスカラー関数\(f(\bs{r})\)の勾配と呼ぶ。
発散がスカラーなのに対し、勾配はベクトルであり、また、発散がベクトル\(\bs{V}\)と\(\nabla\)との内積を取る演算であるのに対し、 勾配はスカラー\(f\)に\(\nabla\)を掛ける演算になります。
ちなみに、\(f(\bs{r})\)の引数は\(\bs{r}=(x,y,z)\)という略記です。ベクトルを引数に持つと考えても いいですが、引数がベクトルだからといって、\(f\)がベクトルになるとは限りません。また、\(f\)がスカラーな 関数を特にスカラー関数と呼んでいます。
勾配について詳しくは、スカラーの勾配の記事からどうぞ。