ベクトルの回転
ベクトル\(V(\bs{r})\)に対し、 \begin{eqnarray} \label{rotcomponent} \nabla \times \bs{V}(\bs{r})=\left( \begin{array}{c} \pdiff{V_{z}}{y}-\pdiff{V_{y}}{z} \\ \pdiff{V_{x}}{z}-\pdiff{V_{z}}{x} \\ \pdiff{V_{y}}{x}-\pdiff{V_{x}}{y} \end{array} \right) \end{eqnarray} をベクトルの回転と呼ぶ。
ベクトルの回転も発散と並んで電磁気でよく顔をだします。発散と比べてイメージがしにくいですが、 できるだけ腑に落ちるように説明していきます。
(\ref{rotcomponent})式はデカルト座標基底の成分表示であり、基底ベクトルを使うと \begin{eqnarray} & & \nabla \times \bs{V}(\bs{r}) \nonumber \\ &=& \Bigl( \pdiff{V_{z}}{y}-\pdiff{V_{y}}{z} \Bigr) \bs{e}_{x} + \Bigl( \pdiff{V_{x}}{z}-\pdiff{V_{z}}{x}\Bigr) \bs{e}_{y} + \Bigl(\pdiff{V_{y}}{x}-\pdiff{V_{x}}{y} \Bigr) \bs{e}_{z} \end{eqnarray} とも書けます。(成分表示や基底表示についてはベクトルの基本事項参照。)
ちなみに、回転のことを\(\mathrm{rot} \)を使って \(\nabla \times \bs{V}(\bs{r}) = \mathrm{rot} \boldsymbol{V}\)とも表したりしますが、 両者は同じ意味です。
具体例(レベル1)
具体例を通して直感を養いましょう。
具体例その1
\(a\)を定数として\(V(\bs{r})=a \bs{r}\)を考える。これの発散は \begin{equation} \nabla \times (a \bs{r})= 0 \end{equation} である。
後述するように、回転はベクトルの渦を表します。、 \(a \bs{r}\)は図示すると、ベクトルが原点から放射状に出ているだけで、渦はありません。 そのため、\(a \bs{r}\)の回転は\(0\)というわけです。渦はない一方、湧き出しはあるため ベクトルの発散を取ると値を返します。
また、回転は微分なので、定数ベクトル\(V(\bs{r})=\bs{c}\)に対し \(\nabla \times \bs{c}=0\)です。これは定数ベクトルを図示しても、(回転のない)ただの流れにしか 見えないことに対応しています。
具体例その2
等速円運動の速度ベクトル \begin{eqnarray} \label{rotvec} \bs{v}(\bs{r})=\left( \begin{array}{c} -\omega y \\ \omega x \\ 0 \\ \end{array} \right) \end{eqnarray} の回転を考える。計算するとこれは以下のようになる。 \begin{eqnarray} \label{rotrotvec} \nabla \times \bs{v}(\bs{r})=\left( \begin{array}{c} 0 \\ 0 \\ 2\omega \end{array} \right) \end{eqnarray}
速度ベクトル\(\bs{v} = r \omega \bs{e}_{\theta}\)の回転は\(z\)方向に値を持ちます。 円運動の速度ベクトルは図示すると回転そのものなので、\(\nabla \times \bs{v}(\bs{r})\)が 値を持つことは直感と合致しています。
\(\nabla \times \bs{v}(\bs{r})\)の向きは回転軸を表しています。実際、(\ref{rotvec})式 は\(z\)軸を中心とした円運動を表していますが、その回転(\ref{rotrotvec})式もまた\(z\)成分にのみ値を持っています。
最後に、その成分の大きさと符号は回転の速さと回る向き(時計回りか反時計回りか)に 対応しています。(\ref{rotrotvec})式の\(z\)は角速度\(\omega\)に比例しているので、これは直感的に理解できます。
回転の意味(レベル1)
回転とは単位面積あたりのベクトルの渦のことである。
要は例えば川や海での水の流れをベクトルとすると、その渦がベクトルの回転になっているということです。 (「鳴門の渦潮」とか調べると 写真が出てきてイメージがしやすいかも) なぜそうなるのかを図を使って説明していきます。
解説
まず、\(xy\)平面の中で面積\(\Delta S=\Delta x \Delta y\)をもつ微小な長方形を考えます。この長方形は ベクトル場\(\bs{J}(\bs{r})\)の中にあるとします。ここで、長方形の周りを周る経路で \(\bs{J}(\bs{r})\)の周回積分を考えていきます。 (この「周回」積分が、ベクトルの渦に対応します。)
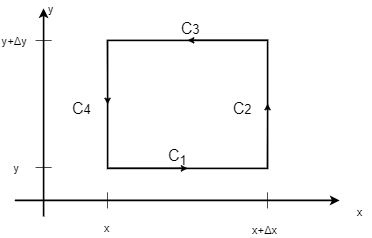
長方形の周囲を反時計回りに回る経路を\(\Delta C\)とおくと、 \begin{eqnarray} \oint_{\Delta C} \bs{J}(\bs{r}) \cdot d \bs{l}&=&\oint_{C_{1}} \bs{J}(\bs{r}) \cdot d \bs{l} +\oint_{C_{2}} \bs{J}(\bs{r}) \cdot d \bs{l} \nonumber \\ &+&\oint_{C_{3}} \bs{J}(\bs{r}) \cdot d \bs{l} +\oint_{C_{4}} \bs{J}(\bs{r}) \cdot d \bs{l} \end{eqnarray} のように、長方形の四辺それぞれに対応する、\(C_{1},C_{2},C_{3},C_{4}\)の経路の線積分に分解できます。
それぞれの辺について、積分を実行していきましょう。まず、\(x\)軸に平行な経路\(C_{1}\)と\(C_{3}\)について線積分 先に実行します。混乱を避けるため、積分変数を\(x\)ではなく、\(x'\)と強調して書くことにします。
経路\(C_{1}\)、\(C_{3}\)ともに、\(x\)から\(x+\Delta x\)まで伸びてますが、積分する方向が互いに逆方向なことに 注意してください。 また、経路\(C_{1}\)の\(y\)座標は「\(y\)」であり、一方、経路\(C_{3}\)の\(y\)座標は「\(y+\Delta y\)」であることを踏まえて計算していくと \begin{eqnarray} & \ &\oint_{C_{1}} \bs{J}(\bs{r}) \cdot d \bs{l} +\oint_{C_{3}} \bs{J}(\bs{r}) \cdot d \bs{l} \nonumber \\ &=& \int_{x}^{x+ \Delta x} J_{x}(x',y,z) dx'\nonumber \\ & \ &+\int_{x+ \Delta x}^{x} J_{x}(x',y+\Delta y,z) dx' \nonumber \\ &=&\int_{x}^{x+ \Delta x} J_{x}(x',y,z) dx'\nonumber \\ & \ &-\int_{x}^{x+ \Delta x} J_{x}(x',y+\Delta y,z) dx' \end{eqnarray} のようにできます。ここで、もし\( \Delta x\)が十分短ければ、積分の中の\(J_{x}(x',y,z)\)を 経路の中間地点\(x'=x+\frac{\Delta x}{2}\)の値で近似して積分の外へだすことができます。 \(J_{x}(x',y+\Delta y,z)\)についても同様の近似を行いましょう。 (厳密にはテイラー展開する必要があります →積分中のテイラー展開)
この近似を使うと、残りの計算は、 \begin{eqnarray} &=& J_{x}(x+\frac{\Delta x}{2},y,z)\int_{x}^{x+ \Delta x} dx' \nonumber \\ & \ &-J_{x}(x+\frac{\Delta x}{2},y+\Delta y,z)\int_{x}^{x+ \Delta x} dx' \nonumber \\ &=& \left\{ J_{x}(x+\frac{\Delta x}{2},y,z) \right. \nonumber \\ & \ & \left. -J_{x}(x+\frac{\Delta x}{2},y+\Delta y,z) \right\} \Delta x \end{eqnarray} となります。
続いてこれを\(y\)軸に平行な経路、\(C_{2}\)と\(C_{4}\)について同じことをやると、 \begin{eqnarray} & \ &\oint_{C_{2}} \bs{J}(\bs{r}) \cdot d \bs{l} +\oint_{C_{4}} \bs{J}(\bs{r}) \cdot d \bs{l} \nonumber \\ &=&\int_{y}^{y+ \Delta y} J_{y}(x+\Delta x,y',z) dy'\nonumber \\ & \ &+\int_{y+ \Delta y}^{y} J_{y}(x,y',z) dy' \nonumber \\ &=& \left\{J_{y}(x+\Delta x,y+\frac{\Delta y}{2},z) \right. \nonumber \\ & \ & \left. -J_{y}(x,y+\frac{\Delta y}{2},z) \right\}\Delta y \end{eqnarray} を得ます。
以上よりこれらを合算すると、 \begin{eqnarray} & \ &\oint_{\Delta C} \bs{J}(\bs{r}) \cdot d \bs{l} \nonumber \\ &=&\frac{1}{\Delta y} \left\{J_{x}(x+\frac{\Delta x}{2},y,z) \right. \nonumber \\ &\quad& \left. -J_{x}(x+\frac{\Delta x}{2},y+\Delta y,z) \right\} \Delta x \Delta y \nonumber \\ &+&\frac{1}{\Delta x} \left\{J_{y}(x+\Delta x,y+\frac{\Delta y}{2},z) \right. \nonumber\\ &\quad& \left. -J_{y}(x,y+\frac{\Delta y}{2},z) \right\}\Delta y \Delta x \nonumber\\ \tolim{\Delta x,\Delta y}{0} & \ &[\pdiff{J_{y}}{x}(\bs{r})-\pdiff{J_{x}}{y}(\bs{r})] \Delta S \nonumber \\ &=&[\nabla \times \bs{J}(\bs{r})]_{z} \Delta S \end{eqnarray} のように回転の\(z\)成分がでてきます。以上により、 \begin{equation} [\nabla \times \bs{J}(\bs{r})]_{z}= \frac{1}{\Delta S } \oint_{\Delta C} \bs{J}(\bs{r}) \cdot d \bs{l} \end{equation} となって、回転の\(z\)成分が、\(xy\)平面における単位面積あたりの渦に対応していることが確認できました。 \(x\)成分、\(y\)成分については、\(yz\)平面、\(zx\)平面での渦に対応しています。
極座標の表式(レベル2)
回転は三次元の極座標(球面座標)において、以下で表される。 \begin{eqnarray} & &\nabla \times \bs{V}(\bs{r}) \nonumber \\ &=& \frac{1}{r \sin \theta}\Bigl( \pdiff{}{\theta}(\sin \theta V_{\phi})-\pdiff{V_{\theta}}{\phi} \Bigr) \bs{e}_{r} \nonumber \\ &+& \frac{1}{r} \Bigl( \frac{1}{\sin \theta}\pdiff{V_{r}}{\phi}-\pdiff{}{r}(rV_{\phi}) \Bigr) \bs{e}_{\theta} \nonumber \\ \label{3polor} &+& \frac{1}{r}\Bigl(\pdiff{}{r}(r V_{\theta})-\pdiff{V_{r}}{\theta} \Bigr) \bs{e}_{\phi} \end{eqnarray} (ただし、\(r \neq 0\)とする)
回転の極座標表示です。デカルト座標の時と大きく見た目が変化しているのは、極座標の基底ベクトル\(\bs{e}_{r},\bs{e}_{\theta},\bs{e}_{\phi}\)も 微分されるので、その寄与が入るからです。
レビチビタ記号での表記(レベル2)
ベクトル\(V(\bs{r})\)に対し、 \begin{equation} \left[ \nabla \times \bs{V} \right]_{i}=\sum_{jk} \varep_{ijk}\pdiff{V_{x_{k}}}{x_{j}} \end{equation} をベクトルの回転と呼ぶ。(ただし、\(x_{1}=x,x_{2}=y,x_{3}=z\))
ベクトルの回転は\(\nabla\)との外積なので、レビチビタ記号を使ってスマートに表すことができます。 アインシュタインの規約などを使ってもう少し簡潔にかくと、 \begin{equation} \left[ \nabla \times \bs{V} \right]_{i}=\varep_{ijk} \partial_{j} V_{k} \end{equation} になります。