ストークスの定理
ベクトル場\(\bs{B}(\bs{r})\)について \begin{equation} \label{Stokestheorem} \int_{S} \nabla \times \bs{B} (\bs{r})\cdot \bs{n}(\bs{r})\mathrm dS = \oint_{C} \boldsymbol{B}(\boldsymbol{r}) \cdot d \boldsymbol{l} \tag{1} \end{equation} が成り立つ。これをストークスの定理と呼ぶ。
ベクトル解析の重要な定理である、ストークスの定理の解説をしていきます。 式中の\(\nabla \times \bs{B}(\bs{r})\)は\(\bs{B}(\bs{r})\)の回転です。 (回転について未習の人はベクトルの回転からどうぞ)
ちなみに、左辺の\(dS\)は面積分、右辺の\(d\bs{l}\)は線積分を表します。\(\bs{n}(\bs{r})\)は 積分面に垂直な単位ベクトルで、\(\nabla \times \bs{B} \cdot \bs{n}(\bs{r})\)は ベクトル\(\nabla \times \bs{B}(\bs{r})\)のうち、積分面に垂直な成分ということになりますね。
また、\(\oint\)は、線積分の中でも特に、周回積分(一周して元の位置に戻ってくる経路の積分) を表していています。
定理の意味(レベル1)
ある領域におけるベクトルの渦の総和は、外淵に沿ったベクトルの和に等しい。
直感的なストークスの定理の説明です。ベクトルの回転がベクトルの渦を意味することを踏まえると このような解釈になります。(回転の意味について詳しくはこちらから)
この定理が言っていることをさらにかみ砕くと、下の図のように、 小さい渦が集まると、大きな渦になるという当然の主張になります。
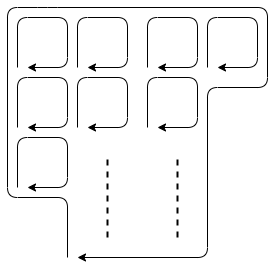
証明(レベル1)
上のイメージを念頭に、より厳密に議論してききます。
証明
まずは式(\ref{Stokestheorem})が微小な長方形に対して成り立つことを示す。 (この部分の論理は途中までベクトルの回転にも載せてあるので、既習の人は飛ばして構わない)
微小な面積\( \Delta S=\Delta x \Delta y \)を持つ下図のような長方形を考える。 これがベクトル場\(\bs{B}(\bs{r})\)の中にあるとする。
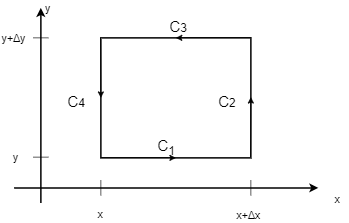
長方形の周囲を反時計回りに回る経路を\(\Delta C\)とおくと、 \begin{eqnarray} \oint_{\Delta C} \bs{B}(\bs{r}) \cdot d \bs{l}&=&\int_{C_{1}} \bs{B}(\bs{r}) \cdot d \bs{l} +\int_{C_{2}} \bs{B}(\bs{r}) \cdot d \bs{l} \nonumber \\ &+&\int_{C_{3}} \bs{B}(\bs{r}) \cdot d \bs{l} +\int_{C_{4}} \bs{B}(\bs{r}) \cdot d \bs{l} \end{eqnarray} のように、長方形の四辺それぞれに対応する、\(C_{1},C_{2},C_{3},C_{4}\)の経路の線積分に分解することができる。
それぞれの辺について、積分を実行していく。まず、\(x\)軸に平行な経路\(C_{1}\)と\(C_{3}\)について線積分 先に実行する。経路\(C_{1}\)の\(y\)座標は「\(y\)」であり、一方、経路\(C_{3}\)の\(y\)座標は「\(y+\Delta y\)」であることを踏まえて計算していくと \begin{eqnarray} & \ &\int_{C_{1}} \bs{B}(\bs{r}) \cdot d \bs{l} +\int_{C_{3}} \bs{B}(\bs{r}) \cdot d \bs{l} \nonumber \\ &=& \int_{x}^{x+ \Delta x} B_{x}(x,y,z) dx\nonumber \\ & \ &+\int_{x+ \Delta x}^{x} B_{x}(x,y+\Delta y,z) dx\nonumber \\ &=&\int_{x}^{x+ \Delta x} B_{x}(x,y,z) dx\nonumber \\ & \ &-\int_{x}^{x+ \Delta x} B_{x}(x,y+\Delta y,z) dx \end{eqnarray} のように変形できる。
ここで、\(B_{x}(x,y,z)\)は定数ではないが、十分積分領域が微小ならば
平均して経路のど真ん中での値、\(B_{x}(x+\frac{\Delta x}{2},y,z)\)で一定値をとるものとして近似し、積分の外へ
出すことができる。(厳密にはテイラー展開する必要があります→積分中のテイラー展開)
\(B_{x}(x,y+\Delta y,z)\)にも同様の近似を施すと、
\begin{eqnarray}
&=&B_{x}(x+\frac{\Delta x}{2},y,z)\int_{x}^{x+ \Delta x} dx \nonumber \\
& \ &-B_{x}(x+\frac{\Delta x}{2},y+\Delta y,z)\int_{x}^{x+ \Delta x} dx' \nonumber \\
&=& \left\{ B_{x}(x+\frac{\Delta x}{2},y,z) \right. \nonumber \\
& \ & \left. -B_{x}(x+\frac{\Delta x}{2},y+\Delta y,z) \right\} \Delta x
\end{eqnarray}
を得る。
続いてこれを\(y\)軸に平行な経路、\(C_{2}\)と\(C_{4}\)について同じことをやると、 \begin{eqnarray} & \ &\int_{C_{2}} \bs{B}(\bs{r}) \cdot d \bs{l} +\int_{C_{4}} \bs{B}(\bs{r}) \cdot d \bs{l} \nonumber \\ &=&\int_{y}^{y+ \Delta y} B_{y}(x+\Delta x,y,z) dy \nonumber \\ & \ &+\int_{y+ \Delta y}^{y} B_{y}(x,y,z) dy \nonumber \\ &=& \left\{B_{y}(x+\Delta x,y+\frac{\Delta y}{2},z) \right. \nonumber \\ & \ & \left. -B_{y}(x,y+\frac{\Delta y}{2},z) \right\}\Delta y \end{eqnarray} を得る。
以上よりこれらを合算すると、 \begin{eqnarray} & \ &\oint_{\Delta C} \bs{B}(\bs{r}) \cdot d \bs{l} \nonumber \\ &=&\frac{1}{\Delta y} \left\{B_{x}(x+\frac{\Delta x}{2},y,z) \right. \nonumber \\ &\quad& \left. -B_{x}(x+\frac{\Delta x}{2},y+\Delta y,z) \right\} \Delta x \Delta y \nonumber \\ &+&\frac{1}{\Delta x} \left\{B_{y}(x+\Delta x,y+\frac{\Delta y}{2},z) \right. \nonumber\\ &\quad& \left. -B_{y}(x,y+\frac{\Delta y}{2},z) \right\}\Delta y \Delta x \nonumber\\ \tolim{\Delta x,\Delta y}{0} & \ &[\pdiff{B_{y}}{x}(\bs{r})-\pdiff{B_{x}}{y}(\bs{r})] \Delta S \nonumber \\ &=&[\nabla \times \bs{B}(\bs{r})]_{z} \Delta S \end{eqnarray} のように回転の\(z\)成分がでてくる。
この形は実は式(\ref{Stokestheorem})の面積分になっている。図1の長方形に垂直な単位ベクトルは\(z\)方向を向いているため、 微小な長方形\(\Delta S\)上において、 \begin{eqnarray} & \ &\int_{\Delta S} \nabla \times \bs{B}(\bs{r}) \cdot \bs{n}(\bs{r}) \mathrm dS \nonumber \\ &=&\int_{\Delta S} [\nabla \times \bs{B}(\bs{r})]_{z} \mathrm dS \nonumber \\ &=&[\nabla \times \bs{B}(x+ \frac{\Delta x}{2},y+ \frac{\Delta y}{2},z)]_{z} \int_{\Delta S} \mathrm dS \nonumber \\ \tolim{\Delta y \Delta x}{0}& \ & [\nabla \times \bs{B}(\bs{r})]_{z} \Delta S \end{eqnarray} が成り立つ。
このことから、微小な長方形に対しては式(\ref{Stokestheorem})が成り立っていることが確認できた。
つづいて、微小でない一般の領域面を考える。ガウスの定理の時と同じように、どんな形状の面であれ、十分小さな長方形をパズルのように並べれば、 その領域面を再現可能である。微小な各長方形に対し、式(\ref{Stokestheorem})は成り立つのだから、 \begin{eqnarray} &\sum_{i} \oint_{\Delta C_{i}} \bs{B}(\bs{r}) \cdot d \bs{l} \nonumber \\ &=\sum_{i} \int_{\Delta S_{i}} \nabla \times \boldsymbol{B}(\boldsymbol{r}) \cdot \boldsymbol{n}(\boldsymbol{r})\mathrm dS \\ \end{eqnarray} が成り立つ。左辺については、長方形の隣り合う辺上では積分は逆向きかつ同じ大きさゆえに相殺されるので、 残るのは隣り合う辺がない領域の外淵の積分に限り、これは式(\ref{Stokestheorem})の左辺に等しい。 一方、右辺についてはそのまま式(\ref{Stokestheorem})の右辺に一致する。
以上から、一般の領域面でも式(\ref{Stokestheorem})が成り立つことが証明できた。