基底ベクトルの微分
基底ベクトルの微分は\(0\)とは限らない
ベクトルを微分するうえで、基底ベクトルの微分は重要です。 なぜなら、\(\bs{r}(t)=r_{1} \bs{e}_{1}+r_{2} \bs{e}_{2}+r_{3} \bs{e}_{3}\)を微分すると、 \begin{eqnarray} \dot{\bs{r}}=\dot{r}_{1} \bs{e}_{1}+\dot{r}_{2} \bs{e}_{2}+\dot{r}_{3} \bs{e}_{3} \nonumber \\ +r_{1} \dot{\bs{e}}_{1}+r_{2} \dot{\bs{e}}_{2}+r_{3} \dot{\bs{e}}_{3} \end{eqnarray} のように明らかに基底ベクトルの微分が出てくるからです。 (基底ベクトルの定義や、これを使った表式についてはベクトルの基本事項の記事参照。)
ここでは基底ベクトルの微分について、座標ごとにまとめました。
デカルト座標の場合(レベル1)
デカルト座標の基底ベクトルの微分は\(0\)つまり \begin{equation} \frac{d \bs{e}_{x}}{dt}=\frac{d \bs{e}_{y}}{dt}=\frac{d \bs{e}_{z}}{dt}=0 \end{equation}
デカルト座標の微分は\(0\)です。 \(0\)なので、今まで基底ベクトルの微分は考えて来なかった わけです。
ちなみに、なぜ\(0\)かというと、時間\(t\)で物体は運動しますが、座標軸の向きは極座標と違って 変わらないからです。
極座標の場合(レベル1)
極座標の基底ベクトルの微分は以下で与えられる \begin{eqnarray} \label{rbasis} \frac{d \bs{e}_{r}}{dt}&=& \omega \bs{e}_{\theta} \\ \label{thetabasis} \frac{d \bs{e}_{\theta }}{dt}&=& - \omega \bs{e}_{r} \end{eqnarray} ただし、\(\omega\)は角速度で、即ち\(\omega=\dot{\theta}\)である。
極座標の基底ベクトルの微分です。極座標の運動方程式の導出にも使います。 極座標では物体の運動とともに軸や基底ベクトルが回転します。なので基底ベクトルの時間微分 も考えなければなりません。
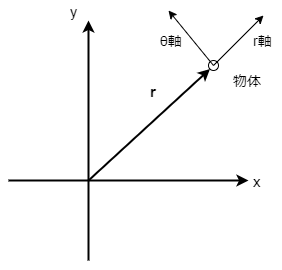
今回は図を使って幾何的に証明する方法と、成分表示を利用する方法の 二つを紹介します。
導出(幾何的な方法)
まず、基底ベクトルの微分を定義通りに書いてみます。 \begin{eqnarray} \label{def} \frac{d \bs{e}_{r}}{dt}(t)=\underset{\Delta t \to 0}{ \lim} \frac{\bs{e}_{r}(t+\Delta t)-\bs{e}_{r}(t)}{\Delta t} \end{eqnarray} これの計算を図を使って解釈し、(\ref{rbasis})式を導きます。 同様にして(\ref{thetabasis})式も導きます。
下図のような単位円を考える。 \(\bs{e}_{r}(t+\Delta t)\)と\(\bs{e}_{r}(t)\) の差を表すベクトルに注目しよう。まず、これの方向 は円の接線方向、即ち\(\theta\)方向であり、 \(\bs{e}_{\theta}\)に平行である。
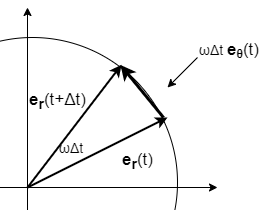
つづいてこのベクトルの大きさについて考える。ラジアンの定義から、 この大きさは角速度\(\omega=\dot{\theta}\)を考えると、大きさは \(\omega \Delta t\)である。ゆえに \begin{equation} \bs{e}_{r}(t+\Delta t)-\bs{e}_{r}(t)=\omega \Delta t \end{equation} である。両辺\(\Delta t\)で割って\(\Delta t \to 0\)の極限を 取ると、(\ref{def})式の左辺に一致し、以上より \begin{equation} \frac{d \bs{e}_{r}}{dt}= \omega \bs{e}_{\theta} \tag{\ref{rbasis}} \end{equation} を得る。
続いて、再び同じように下図のような単位円を考える。
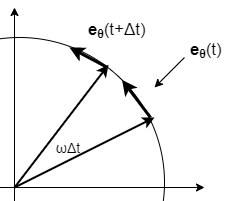
\(r\)の時と同じように\(\bs{e}_{\theta}(t+\Delta t)\)と \(\bs{e}_{\theta}(t)\)の差を表すベクトルに注目しよう。 上の図では少し見づらいので、ふたつのベクトルを平行移動させた 図を以下に示す。
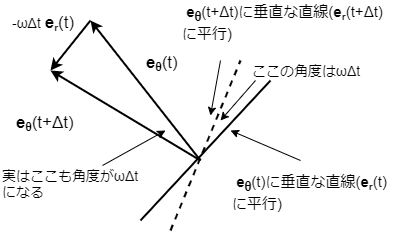
まず、ベクトル\(\bs{e}_{\theta}(t+\Delta t)\)と \(\bs{e}_{\theta}(t)\)の差は、図より\(r\)の逆方向、つまり\(\bs{e}_{r}(t)\) に比例する。
加えて、図のように二つの基底の法線方向の直線を考える。 これらの直線は図1より明らかなように、\(\bs{e}_{r}(t+\Delta t)\)と\(\bs{e}_{r}(t)\) にそれぞれ平行であって、ゆえにその間の角度は\(\omega \Delta t\)である。
さらに、幾何的考察から、\(\bs{e}_{\theta}(t+\Delta t)\)と \(\bs{e}_{\theta}(t)\)のなす角度も\(\omega \Delta t\)であるため、 二つのベクトルに内接する単位円を考えれば、差のベクトルの大きさは \(\omega \Delta t\)であると結論できる。
以上から、 \begin{equation} \frac{d \bs{e}_{r}}{dt}= \omega \bs{e}_{\theta} \tag{\ref{thetabasis}} \end{equation} がいえた。
導出(成分を使う方法)
極座標の基底ベクトルをデカルト座標の基底で展開すると \begin{eqnarray} \bs{e}_{r}(t)&=&\cos \theta \bs{e}_{x}+\sin \theta \bs{e}_{y} \\ \bs{e}_{\theta}(t)&=&-\sin \theta \bs{e}_{x}+\cos \theta \bs{e}_{y} \end{eqnarray} のようにかけますが、これを成分表示すると \begin{equation} \label{rdiff} \bs{e}_{r}= \left (\begin{array}{c} \cos \theta \\ \sin \theta \end{array} \right) \end{equation} \begin{equation} \label{thetadiff} \bs{e}_{\theta}= \left (\begin{array}{c} -\sin \theta \\ \cos \theta \end{array} \right) \end{equation} のように表示できます。(証明はこちらから)上でも述べた通り、 デカルト座標の 基底ベクトルは微分が\(0\)なので、この成分表示のもとでは 単に成分ごとに微分をすれば、\(\bs{e}_{r}(t)\) や\(\bs{e}_{\theta}(t)\)の微分を計算できます。
まずは(\ref{rdiff})式の微分から計算する。 \begin{equation} \frac{d \bs{e}_{r}}{dt}(t)= \left (\begin{array}{c} -\sin \theta \ \dot{\theta}\\ \cos \theta \ \dot{\theta} \end{array} \right) \end{equation} より、(\ref{thetadiff})式と見比べて、 \begin{equation} \frac{d \bs{e}_{r}}{dt}= \dot{\theta} \bs{e}_{\theta} \end{equation} であって、ここで\(\dot{\theta}=\omega\)だったので (\ref{rbasis})式がいえた。
続いて(\ref{thetadiff})式の微分を考える。 \begin{equation} \frac{d \bs{e}_{\theta}}{dt}(t)= \left (\begin{array}{c} -\cos \theta \ \dot{\theta}\\ -\sin \theta \ \dot{\theta} \end{array} \right) \end{equation} より、(\ref{rdiff})式と見比べて、(\ref{thetabasis})式を得る。
球面座標(レベル2)
球面座標の基底ベクトルの時間微分は以下で与えられる \begin{eqnarray} \label{rbasis'} \frac{d \bs{e}_{r}}{dt}&=& \dot{\theta} \bs{e}_{\theta} +\dot{\phi} \sin \theta \ \bs{e}_{\phi} \\ \label{thetabasis'} \frac{d \bs{e}_{\theta }}{dt}&=& - \dot{\theta} \bs{e}_{r} +\dot{\phi} \cos \theta \ \bs{e}_{\phi} \\ \label{phibasis} \frac{d \bs{e}_{\phi}}{dt}&=&-\phi(\sin \theta \ \bs{e}_{r} +\cos \theta \ \bs{e}_{\theta}) \end{eqnarray}
球面座標の時間微分です。おそらくこちらはそう使うことはないと思います。 この式よりも、以下の公式の方が重要です。
球面座標の基底ベクトルの微分は以下の関係を持つ。 \begin{eqnarray} \label{rbasisdiff} \frac{d \bs{e}_{r}}{d \theta} = \bs{e}_{\theta}, \ \frac{d \bs{e}_{r}}{d \phi} = \sin \theta \bs{e}_{\phi} \end{eqnarray} 及び \begin{eqnarray} \label{thetabasisdiff} \frac{d \bs{e}_{\theta}}{d \theta} = -\bs{e}_{r}, \ \frac{d \bs{e}_{\theta}}{d \phi} = \cos \theta \bs{e}_{\phi} \end{eqnarray} 及び \begin{eqnarray} \label{phibasisdiff} \frac{d \bs{e}_{\phi}}{d \theta} = 0, \ \frac{d \bs{e}_{\phi}}{d \phi}= -\sin \theta \bs{e}_{r}-\cos \theta \bs{e}_{\theta} \end{eqnarray} である。(\(r\)微分に関しては全て\(0\))
これらの式を使うと、時間微分について例えば、 \begin{equation} \frac{d \bs{e}_{r}}{dt}= \dot{\theta} \frac{d \bs{e}_{r}}{d \theta} +\dot{\phi} \frac{d \bs{e}_{r}}{d \phi} \end{equation} のように変形し、ここに(\ref{rbasisdiff})式を代入することで計算が可能です。
導出
ここでは基底をデカルト座標による成分表示を利用して導出をします。
まず、 \begin{equation} \label{r} \bs{e}_{r}= \left (\begin{array}{c} \sin \theta \cos \phi \\ \sin \theta \sin \phi \\ \cos \theta \end{array} \right) \end{equation} \begin{equation} \label{theta} \bs{e}_{\theta}= \left (\begin{array}{c} \cos \theta \cos \phi \\ \cos \theta \sin \phi \\ -\sin \theta \end{array} \right) \end{equation} \begin{equation} \label{phi} \bs{e}_{\phi}= \left (\begin{array}{c} -\sin \phi \\ \cos \phi \\ 0 \end{array} \right) \end{equation} である。この表式からすぐに、\(r\)微分をすると\(0\)になることが 分かる。あとは残りの変数\(\theta,\phi\)について、これらを順番に微分していく。(ここではスペースの関係で、\(\bs{e}_{r}\)の微分のみ計算し 他は割愛する。)
実際に計算をしてみると、 \begin{equation} \frac{d \bs{e}_{r}}{d \theta}= \left (\begin{array}{c} \cos \theta \cos \phi \\ \cos \theta \sin \phi \\ -\sin \theta \end{array} \right) \\ =\bs{e}_{\theta} \end{equation} 及び、 \begin{equation} \frac{d \bs{e}_{r}}{d \phi}= \left (\begin{array}{c} -\sin \theta \sin \phi \\ \sin \theta \cos \phi \\ 0 \end{array} \right) \\ =\sin \theta \bs{e}_{\phi} \end{equation} になり、(\ref{rbasisdiff})式が確認できる。