ベクトルの線積分
与えられた経路に沿って行う積分を線積分と呼ぶ。その表式は スカラーかベクトルかで異なり、特に ベクトル関数\(\bs{A}(\bs{r})\)について、以下の積分 \begin{equation} \label{slineint} I= \int_{C} \bs{A}(\bs{r}) \cdot d \bs{r} \end{equation} をベクトル関数の線積分と呼ぶ。ここに\(C\)は 積分する経路を表し、\(d \bs{r}\)は線素ベクトルと呼ばれる積分要素で その定義は \begin{eqnarray} \label{diff} d \bs{r}=\left( \begin{array}{c} dx \\ dy \\ dz \end{array} \right) \end{eqnarray} である。(3次元デカルト座標の場合)
線積分はベクトル解析で必須の計算です。特にベクトルの線積分の方は 物理では仕事や電磁気の計算に頻出します。スカラー関数の線積分については こちらからどうぞ。 ベクトルの線積分について簡単にまとめました。
具体例(レベル1)
線積分が物理で用いられる例を通して、線積分の具体的なイメージを身につけましょう。 具体的なイメージがあれば、理解する助けになります。
具体例その1
力学において、仕事はベクトルの線積分 \begin{equation} \label{work} W= \int_{C} \bs{F} \cdot d\bs{r} \end{equation} で表される。
後述するように、線積分は微小な内積 を経路\(C\)に沿って足し上げる操作です。 つまり、(\ref{work})式は仕事\(W\)が微小な仕事\(\bs{F} \cdot d\bs{r}\) の和として表せることを示しています。
具体例その2
電磁気のアンペールの法則の積分型は線積分によって表される。
\begin{equation} \oint_{C} \bs{B}(\bs{r}) \cdot d \bs{r} = \mu_{0} I \end{equation}線積分は一般には経路に依存し、特に\(\oint_{C}\)は、一周して元の場所へ戻る経路であることを表しています。 この線積分を特に周回積分と呼びます。上の例では、電流の周りを一周する経路を\(C\)と呼んでいて、 電流の周囲に発生した磁場を足し上げています。
定義と意味(レベル1)
ベクトルの線積分 \begin{equation} I= \int_{C} \bs{A}(\bs{r}) \cdot d \bs{r} \tag{\ref{slineint}} \end{equation} とは、端的には経路\(C\)上で、内積\(\bs{A}(\bs{r}) \cdot d \bs{r}\)を 足し合わせる操作である。
ベクトルの線積分の直感的な定義です。抽象的で分かりずらい場合は上の具体例を見れば、 イメージがしやすいと思います。 まずは図1のように、経路\(C\)上にベクトルが生えている状況を考えます。
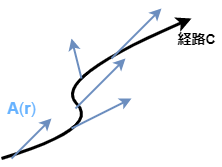
その上で、以下のように経路を近似するようなベクトル\(\Delta \bs{r}\)を 考え、それとの内積\(\bs{A}(\bs{r}) \cdot \Delta \bs{r}\)を足し上げることにします。
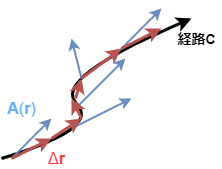
これを\(C\)に沿って行い\(\Delta \bs{r} \to 0\)の極限をベクトルの線積分と呼びます。 以上のイメージを数式で表すと以下のようになります。
線積分は内積\(\bs{A}(\bs{r}) \cdot d \bs{r}\)を 足し合わせる操作であり、和の記号を使って書くと \begin{equation} \int_{C} \bs{A}(\bs{r}) \cdot d\bs{r} = \lim_{\Delta \bs{r}_{i} \to 0}\sum_{i=1}^{\infty} \bs{A}(\bs{r}_{i}) \cdot \Delta \bs{r}_{i} \end{equation} の通り。(ただし、\(\Delta \bs{r}_{i}\)は、経路\(C\)を細かく分割してベクトルで表したもの)
計算方法(レベル1)
線積分は媒介変数表示によって計算が可能。
スカラーの線積分にせよ、ベクトルの線積分にせよ、基本的に線積分は 媒介変数表示しなければ計算ができないので注意が必要です。 媒介変数による積分は以下のようにまとめられます。
一般に、経路\(C\)の媒介変数表示は、3次元の場合\(x=x(t)\)、\(y=y(t)\)、\(z=z(t)\) の形で与えられる。線素ベクトル\(d\bs{r}\)は \begin{eqnarray} d\bs{r} = \frac{d \bs{r}}{dt} dt \end{eqnarray} となるので、線積分は以下のように媒介変数表示で 計算ができる。 \begin{eqnarray} & \ & \int_{C} \bs{A}(\bs{r}) \cdot d\bs{r} \nonumber \\ & \ & = \int_{t_{i}}^{t_{f}} \bs{A}(\bs{r}(t)) \cdot \frac{d\bs{r}}{dt} dt \nonumber \\ \label{paradisplay} & \ & = \int_{t_{i}}^{t_{f}} \left(A_{x}(\bs{r}(t)) \frac{dx}{dt} + A_{y}(\bs{r}(t))\frac{dy}{dt}+A_{z}(\bs{r}(t))\frac{dz}{dt}\right) dt \end{eqnarray} ただし、\(t_{i},t_{f}\)は経路の始点と終点に 対応する\(t\)の値であり、\(A_{x}(\bs{r}),A_{y}(\bs{r}),A_{z}(\bs{r})\)はそれぞれ\(\bs{A}(\bs{r})\)の \(x\)成分、\(y\)成分及び\(z\)成分。2次元の場合も同様に媒介変数表示で計算ができる。
上の内容を要約すると、線積分は以下の3ステップで実行できるということです。
(ステップ1)経路\(C\)を媒介変数表示で表す。
(ステップ2)線素ベクトル\(d\bs{r}\)を媒介変数\(t\)で表す。
(ステップ3)線積分を媒介変数\(t\)の積分(\ref{paradisplay})へ帰着し、実行する。
それでは例題を通して、どのように線積分が計算されるか追っていきましょう。
例題その1
\(C\)を\(x\)軸に沿った長さ\(l\)の直線とする。進むのは正の方向とする。 このもとで \begin{equation} I_{1}= \int_{C} \bs{A}(\bs{r}) \cdot d\bs{r} \end{equation} を計算したい。ただし\(k\)を正の定数として \begin{eqnarray} \bs{A}(\bs{r})=\left( \begin{array}{c} -kx \\ 0 \\ 0 \end{array} \right) \end{eqnarray} とする。
経路が単純な場合を例に、計算の流れをつかみましょう。
計算
まず、ステップ1として経路\(C\)を媒介変数表示で表す。 今回の場合は\(C\)が\(x\)に沿った直線なので \(v\)を適当な定数として \begin{eqnarray} x(t)=vt \quad (0 \leq t \leq \frac{l}{v}) \\ y(t)=0 \quad (0 \leq t \leq \frac{l}{v}) \\ z(t)=0 \quad (0 \leq t \leq \frac{l}{v}) \end{eqnarray} と表せる。(実は、最終的な結果は\(v\)に依存しないので単に\(v=1\)として \(x=t\)などと表してもよい。) 後でステップ3で使うので、\(t\)の定義域も忘れずに調べておく。
続いてステップ2であるが、ステップ1の結果より線素ベクトルは \begin{eqnarray} d\bs{r} &=& \frac{d \bs{r}}{dt} dt \nonumber \\ &=& \left( \begin{array}{c} v dt \\ 0 \\ 0 \end{array} \right) \end{eqnarray} である。あとは、ステップ3として (\ref{paradisplay})式を使えばよい。実際にやってみると (\((x(t),y(t),z(t))=(vt,0,0)\)に注意して) \begin{eqnarray} & \ & \int_{C} \bs{A}(\bs{r}) \cdot d\bs{r} \nonumber \\ & \ & =\int_{0}^{\frac{l}{v}} A_{x}(\bs{r}(t)) \frac{dx}{dt} dt \nonumber \\ & \ & =\int_{0}^{\frac{l}{v}} -kvt \ v dt \nonumber \\ & \ & = -\frac{1}{2}kl^2 \end{eqnarray} となり以上より積分結果 \(\int_{C} \bs{A}(\bs{r}) \cdot d\bs{r}= -\frac{1}{2}kl^2\) を得る。
この例題では、直感的に内積\(\bs{A}(\bs{r}) \cdot d\bs{r} = -kx \ dx\) を取って、適当な積分範囲をあてがえば \begin{equation} \int_{C} \bs{A}(\bs{r}) \cdot d\bs{r} = \int_{-l}^{l} A_{x} dx \end{equation} のようにしても正しく計算はできてしまいます。ただし、この方法が有効なのは、 今回のような経路が単純な場合に限るので注意してください。
線積分をデカルト座標で計算するとき、経路\(C\)
が直線に分割できるならば、
適当な積分範囲を取ることで直感的に計算ができる。
しかし、一般には \begin{equation} \int_{C} \bs{A} \cdot d \bs{r} \neq \int A_{x} dx+\int A_{y} dy + \int A_{z} dz \end{equation} なことに注意。
(\ref{deconposite})式が成り立たない典型的な例として、円のような曲線が経路になっている時が挙げられます。 この場合は、媒介変数を使わなければ正しい結果は得られません。
例題その2
経路\(C\)を\(x^2+y^2=a^2\)の円を反時計周りに一周する軌跡 として、以下の線積分を実行したい。
\begin{equation} I_{2}= \int_{C} \bs{A} \cdot d\bs{r} \end{equation} を計算したい。ただし\(k\)を正の定数として \begin{equation} \bs{A}=\left (\begin{array}{c} -k y \\ k x\\ 0 \end{array} \right) \end{equation} とする。計算
まず、ステップ1として経路\(C\)を媒介変数表示で表す。今回は軌跡が円なので、 \(\omega\)を適当な定数として、 \begin{eqnarray} x(t)=a \cos \omega t \quad (0 \leq t \leq \frac{2 \pi}{\omega}) \\ y(t)=a \sin \omega t \quad (0 \leq t \leq \frac{2 \pi }{\omega }) \\ z(t)=0 \quad (0 \leq t \leq \frac{2 \pi }{\omega }) \end{eqnarray} と表せる。(最終的な結果は\(\omega\)に依存しないので単に\(\omega=1\)として \(x=a \cos t,y=a \sin t\)などと表してもよい。) 後でステップ3で使うので、\(t\)の定義域も忘れずに調べておく。
続いてステップ2であるが、ステップ1の結果より線素ベクトルは \begin{eqnarray} d\bs{r} &=& \frac{d \bs{r}}{dt} dt \nonumber \\ &=& \left( \begin{array}{c} -a\omega \sin \omega t dt\\ a\omega \cos \omega t dt \\ 0 \end{array} \right) \end{eqnarray} である。あとは、ステップ3として (\ref{paradisplay})式を使えばよい。実際にやってみると \begin{eqnarray} & \ & \int_{C} \bs{A}(\bs{r}) \cdot d\bs{r} \nonumber \\ & \ & =\int_{0}^{\frac{2 \pi}{\omega}} (k a^2 \sin^2 \omega t + k a^2 \cos^2 \omega t) \omega dt \nonumber \\ & \ & =\int_{0}^{2 \pi} ka^2 d (\omega t) \nonumber \\ & \ & =2 \pi ka^2 \end{eqnarray} となり以上より積分結果 \(\int_{C} \bs{A}(\bs{r}) \cdot d\bs{r}=2\pi ka^2\) を得る。
特殊なパターンとして、線積分が途中の経路に依存せず、始点と終点のみで一意に定まる場合があります。 物理では、保存力の仕事がこれにあたります。この場合は、経路を勝手に変更し、計算しやすい経路で 計算が可能です。後述するように、このパターンには判別法があります。
線積分\(I= \int_{C} \bs{A}(\bs{r}) \cdot d \bs{r}\) について、 \begin{equation} \label{rot0} \nabla \times \bs{A} =0 \end{equation} が成り立つ時、\(I_{\bs{A}}\)は途中の経路によらない。
この性質の証明は下のギモン参照。保存力は物理では頻出なので、 線積分を実行するときは事前に(\ref{rot0})式が成り立っているか確かめておきましょう。
例題その3
原点を中心とした、半径\(a\)の半円の弧そった経路を\(C\)とする。 (ただし反時計回り)このもとで \begin{equation} I_{3}= \int_{C} \bs{A}(\bs{r}) \cdot d\bs{r} \end{equation} を計算したい。ただし、 \begin{equation} \bs{A}=\left (\begin{array}{c} \frac{A}{r^3} x \\ \frac{A}{r^3} y \\ \frac{A}{r^3} z \end{array} \right) \end{equation} とする。
計算
\(\bs{A}\)の表式より、 \begin{equation} \nabla \times \bs{A} =0 \end{equation} が成り立つ。実際、\(\bs{A} = - \nabla \frac{A}{r}\)のように\(\bs{A}\)は表すことができ、 勾配の回転は\(0\)なのでこれは正しい。
ゆえに、\(I_{3}\)は、始点と終点さえ同じであれば、途中の経路にはよらない。 もともとの経路は原点を中心とする半円だから、 始点と終点は\(x\)軸上の\((a,0,0),(-a,0,0)\)と定めれば問題ない。
始点と終点を直線で結ぶ経路を\(C'\)と置く。これを媒介変数で表すと \begin{eqnarray} x(t)&=&vt \quad (\frac{a}{v} \leq t \leq \frac{-a}{v}) \\ y(t)&=&0 \quad (\leq \frac{a}{v} \leq t \leq \frac{-a}{v}) \\ z(t)&=&0 \quad (\frac{a}{v} \leq t \leq \frac{-a}{v}) \end{eqnarray} である。(実は、最終的な結果は\(v\)に依存しないので単に\(v=1\)として \(x=t\)などと表してもよい。)
線素ベクトルは \begin{eqnarray} d\bs{r} &=& \frac{d \bs{r}}{dt} dt \nonumber \\ &=& \left( \begin{array}{c} v dt \\ 0 \\ 0 \end{array} \right) \end{eqnarray} なので、線積分は \begin{eqnarray} & \ & \int_{C} \bs{A}(\bs{r}) \cdot d\bs{r} \nonumber \\ & \ & \int_{C'} \bs{A}(\bs{r}) \cdot d\bs{r} \nonumber \\ & \ & =\int_{\frac{a}{v}}^{\frac{-a}{v}} \frac{A}{|vt|^3} vt \ v dt \nonumber \\ & \ & = 0 \end{eqnarray} となる。ただし、最後に奇関数の積分が\(0\)になることを使った。
ちなみに、なぜ\(I_{3}\)が\(0\)になったかというと、\(\bs{A}(\bs{r})\)が(クーロン力などの)中心力に対応しているからです。 これは実際\(\bs{A} = - \nabla \frac{A}{r}\)と書けることからも理解できます。そして、中心力は円弧上で 動かしても仕事は\(0\)です。このため、仕事に対応する線積分\(I_{3}\)は\(0\)というわけです。
さらに他の例題が気になる人は、仕事の計算の記事に飛んでください。 様々なパターンの線積分を考えているので、ここでは扱えなかった問題も解説されています。
さて、ここまでで気が付いた人もいるかもしれませんが、媒介変数の取り方には自由度があります。 例えば上の具体例では、\(x=vt\)や\(x=a \cos \omega t\)などと書きましたが、 最終的な結果は\(v,\omega\)には依存しませんでした。なので、極端な話、\(v=1,\omega=1\)などと勝手にとってよいわけです。
これは、(正しく経路を表していれば)
媒介変数の取り方の詳細には依存しない、という線積分の性質に起因しています。
これの証明については以下を参考。
経路によらない場合(レベル1)
線積分\(I= \int_{C} \bs{A}(\bs{r}) \cdot d \bs{r}\) について、 \begin{equation} \nabla \times \bs{A} =0 \tag{\ref{rot0}} \end{equation} が成り立つ時、\(I\)は途中の経路によらず、始点と終点のみで決まる。
線積分の性質です。線積分が途中の経路に依らないとは、 始点と終点が同じで途中のみが異なる経路\(C_{A}\)と\(C_{B}\)に対して \begin{equation} \label{compareAB} \int_{C_{A}} \bs{A}(\bs{r}) \cdot d \bs{r} = \int_{C_{B}} \bs{A}(\bs{r}) \cdot d \bs{r} \end{equation} ということです。これは、保存力の仕事の性質そのものですね。このため保存力の判定にも 回転が\(0\)かどうかが使われるわけです。
証明
方針として、まずは(\ref{rot0})から、周回積分が\(0\) \begin{equation} \label{oint0} \oint_{C} \bs{A}(\bs{r}) \cdot d \bs{r} = 0 \end{equation} になることを示し、そしてこの式が(\ref{compareAB})と同値であることを確認します。
まず、(\ref{rot0})の両辺を面積分する。 \begin{equation} \int_{S} \nabla \times \bs{A} \cdot \bs{n} dS =0 \end{equation} ここでストークスの定理を使えば \begin{equation} \oint_{C} \bs{A} \cdot d \bs{r} =0 \tag{\ref{oint0}} \end{equation} を得る。ただし、\(\oint_{C}\)は一周してもとに戻ってくる経路での 積分を表す。
ここで、始点と終点が同じで途中のみが異なる経路\(C_{A}\)と\(C_{B}\)を考える。 そして、\(C_{B}\)を逆走する経路を\(C_{-B}\)と置き、 経路\(C_{A}\)を通ったあと、\(C_{-B}\)を通って元の場所へ戻ってくる場合を考える。 これを\(C\)と置くと、 \begin{eqnarray} &&\int_{C_{A}} \bs{A}(\bs{r}) \cdot d \bs{r} + \int_{C_{-B}} \bs{A}(\bs{r}) \cdot d \bs{r} \nonumber \\ &=&\int_{C_{A}+C_{-B}} \bs{A}(\bs{r}) \cdot d \bs{r} \nonumber \\ &=&\oint_{C} \bs{A}(\bs{r}) \cdot d \bs{r} \nonumber \\ \end{eqnarray} 最終行は(\ref{oint0})式より\(0\)になるので \begin{equation} \int_{C_{A}} \bs{A}(\bs{r}) \cdot d \bs{r} + \int_{C_{-B}} \bs{A}(\bs{r}) \cdot d \bs{r} =0 \end{equation} が成り立つ。線積分は逆走すると値が反転するので、これは即ち \begin{equation} \int_{C_{A}} \bs{A}(\bs{r}) \cdot d \bs{r} = \int_{C_{B}} \bs{A}(\bs{r}) \cdot d \bs{r} \tag{\ref{compareAB}} \end{equation} である。
パラメータの取り方の非依存性(レベル2)
線積分は(経路を正しく表せていれば)媒介変数の取り方には依存しない。
上の例題では、例えば媒介変数表示で\(x(t)=vt\)と と表したとしても、最終的な結果に\(v\)が依存しないことが分かります。 つまり、\(v=1\)として\(x=t\)と置いても、\(v=2\)として\(x=2t\)と置いても 線積分の結果は変わらないわけです。 この性質を、線積分は媒介変数の取り方に依らないといいます。 (ただし、その媒介変数が経路を正しく表せている場合の話です)
証明
証明に必要なのは合成関数の微分公式と置換積分くらいなので 簡単に示せます。
まず、経路\(C\)がある媒介変数\(t\)を使って \begin{eqnarray} \bs{r}=\bs{r}(t) \quad (a \leq t \leq b ) \end{eqnarray} と書けるとする。
このもとで、\(t\)とは異なる媒介変数\(s\)を 変数変換\(t=f(s)\)によって導入する。すると、上の表記は \begin{eqnarray} \bs{r}(t)=\bs{r}(f(s))=\tilde{\bs{r}}(s) \quad (a' \leq s \leq b') \end{eqnarray} のようにも表せる。(ただし、\(s\)の定義から \(f(a')=a,f(b')=b\)が成り立つとする。)
この二つの媒介変数を使って、線積分\(\int_{C} \bs{A}(\bs{r}) \cdot d\bs{r}\) の計算をそれぞれ実行してみよう。両者が等しいならば、 媒介変数に依存せず、線積分は一意に値が定まることがいえる。
まず\(t\)で媒介変数表示したものを\(I_{t}\)と置くと \begin{eqnarray} I_{t}=\int_{a}^{b} \bs{A}(\bs{r}(t)) \cdot \frac{d\bs{r}}{dt}(t) \ dt \end{eqnarray} であるが、続いて\(s\)を使って表したものを\(I_{s}\)と 置いてこれを計算すると、 \begin{eqnarray} I_{s}&=&\int_{a'}^{b'} \bs{A}(\tilde{\bs{r}}(s)) \cdot \frac{d\tilde{ \bs{r}}}{ds}(s) \ ds \nonumber \\ &=& \int_{a'}^{b'} \bs{A}(\bs{r}(f(s))) \cdot \frac{d\bs{r}}{dt}(f(s)) \ \frac{dt}{ds} ds \nonumber \\ &=& \int_{a}^{b} \bs{A}(\bs{r}(t)) \cdot \frac{d\bs{r}}{dt} dt \nonumber \\ &=& I_{t} \end{eqnarray} (ただし、途中で合成関数の微分と置換積分の公式を使った)以上より\(I_{s}=I_{t}\)であり 適切に経路をパラメータ化できていれば、線積分は媒介変数の取り方に依らないことが確認できた。