外積とその諸性質
ベクトルの外積とは \begin{eqnarray} \label{Cartesiandiff} \bs{a} \times \bs{b}=\left( \begin{array}{c} a_{y}b_{z}-a_{z}b_{y} \\ a_{z}b_{x}-a_{x}b_{z}\\ a_{x}b_{y}-a_{y}b_{x} \end{array} \right) \end{eqnarray} で表されるベクトル「\(\bs{a} \times \bs{b}\)」のことである。
内積と異なり、外積はベクトルになります。 力学と電磁気でお馴染みの、外積について基本事項をまとめました。
外積の性質(レベル1~2)
外積\(\bs{a} \times \bs{b}\)は、\(\bs{a}\)と\(\bs{b}\)にそれぞれ直交するベクトルである。
下の図のように、外積\(\bs{a} \times \bs{b}\)は\(\bs{a}\)と\(\bs{b}\)にそれぞれ直交します。 (というかそれが定義みたいなものです)
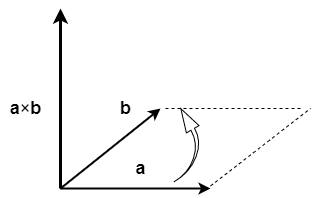
直交しているか確かめるには、\(\bs{a}\)や\(\bs{b}\)との内積をとれば確認できます。 示したい式は \begin{equation} \bs{a} \cdot (\bs{a} \times \bs{b})=\bs{b} \cdot (\bs{a} \times \bs{b})=0 \end{equation} です。
証明
\(\bs{a} \cdot (\bs{a} \times \bs{b})=0\)を示す。
(i)成分表示の場合(レベル1)
\begin{eqnarray} \bs{a} \cdot (\bs{a} \times \bs{b})&=&a_{x}(a_{y}b_{z}-a_{z}b_{y}) \nonumber \\ &+&a_{y}(a_{z}b_{x}-a_{x}b_{z}) \nonumber \\ &+&a_{z}(a_{x}b_{y}-a_{y}b_{x}) \nonumber \\ &=&0 \end{eqnarray}(ii)レビチビタ記号を使う場合(レベル2)
\begin{eqnarray} \bs{a} \cdot (\bs{a} \times \bs{b})&=&\sum_{ijk} \varep_{ijk} a_{i}a_{j}b_{k} \nonumber \\ &=&0 \end{eqnarray}最後の行は反対称な\(\varep_{ijk}\)と対称な\(a_{i}a_{j}\)の積なので0になる。 (レビチビタ表記については下のギモン参照)
\(\bs{b} \cdot (\bs{a} \times \bs{b})=0\)の方も全く同様
\(\bs{a}\)と\(\bs{b}\)の入れ替えに対し、 \begin{equation} \bs{a} \times \bs{b}=-(\bs{b} \times \bs{a}) \end{equation} が成り立つ。
内積では\(\bs{a} \cdot \bs{b}=\bs{b} \cdot \bs{a}\)でしたが、外積では勝手が違います。 この性質から\(\bs{a} \times \bs{a}=-\bs{a} \times \bs{a}\)になるので、自分自身との外積は0( \(\bs{a} \times \bs{a}=0\))という、重要な性質が示せます。
外積\(\bs{a} \times \bs{b}\)の大きさは \begin{equation} \label{outerproduct3} |\bs{a} \times \bs{b}|=|\bs{a}||\bs{b}| \sin \theta \end{equation} である。
図1に描かれている、\(\bs{a}\)と\(\bs{b}\)を二辺とする平行四辺形の面積が、外積の大きさに なっています。真面目に計算しても確かめられますが、骨が折れるので覚えておいた方がいいかもしれません。 一応、証明を置いておきます。
証明
方針として、まず内積と外積を結ぶ公式 \begin{equation} |\bs{a}|^2 |\bs{b}|^2 -(\bs{a} \cdot \bs{b})^2 =|\bs{a} \times \bs{b}|^2 \end{equation} を示します。これが示せれば、\(\bs{a} \cdot \bs{b}=|\bs{a}||\bs{b}| \cos \theta \) なので、(\ref{outerproduct3})が示せたことになります。
外積のレビチビタ表記を使って右辺を変形していく。
(レビチビタ表記については下のギモン参照)
\begin{eqnarray}
|\bs{a} \times \bs{b}|^2&=&\sum_{i}(\sum_{jk} \varep_{ijk} a_{j}b_{k})^2 \nonumber \\
&=&\sum_{i}\sum_{jk}\sum_{lm} \varep_{ijk}\varep_{ilm} a_{j}b_{k}a_{l}b_{m} \nonumber \\
&=&\sum_{jklm} (\delta_{jl}\delta_{km}-\delta_{jm}\delta_{kl})a_{j}b_{k}a_{l}b_{m} \nonumber \\
&=&\sum_{j}a_{j}^2 \sum_{k}b_{k}^2-\sum_{jk} a_{j}b_{j}a_{k}b_{k} \nonumber \\
&=&|\bs{a}|^2 |\bs{b}|^2 -(\bs{a} \cdot \bs{b})^2
\end{eqnarray}
となって示せた。
途中、レビチビタ記号の公式
\begin{equation}
\sum_{i} \varep_{ijk}\varep_{ilm}=\delta_{jl}\delta_{km}-\delta_{jm}\delta_{kl}
\end{equation}
を使いました。
外積の微分(レベル1)
外積の微分は \begin{eqnarray} \frac{d}{dt}(\bs{a} \times \bs{b})=\left(\frac{d \bs{a}}{dt} \right) \times \bs{b}+\bs{a} \times \left(\frac{d \bs{b}}{dt}\right) \end{eqnarray} のように計算ができる。
導出などはベクトルの微分公式(基本編)を参照してください。
具体例(レベル1~2)
外積は力学や電磁気などで多く見かけますが、相対性理論以降は見かけなくなります。
(i)角運動量(\(\bs{L}:=\bs{x} \times \bs{p}\))
\begin{eqnarray} \bs{x}=\left( \begin{array}{c} x \\ y \\ z \end{array} \right) \end{eqnarray} \begin{eqnarray} \bs{p}=\left( \begin{array}{c} p_{x} \\ p_{y} \\ p_{z} \end{array} \right) \end{eqnarray} の時、角運動量\(\bs{L}\)は \begin{eqnarray} \bs{L}=\left( \begin{array}{c} \begin{array}{c} y p_{z}-z p_{y} \\ z p_{x}-x p_{z}\\ x p_{y}-y p_{x} \end{array} \end{array} \right) \end{eqnarray}(ii)ベクトルポテンシャル(\(\bs{B}=\nabla \times \bs{A}\)) \begin{eqnarray} \bs{A}=\left( \begin{array}{c} A_{x} \\ A_{y} \\ A_{z} \end{array} \right) \end{eqnarray} の時、 \begin{eqnarray} \bs{B}=\left( \begin{array}{c} \begin{array}{c} \frac{\partial A_{z}}{\partial y}-\frac{\partial A_{y}}{\partial z} \\ \frac{\partial A_{x}}{\partial z}-\frac{\partial A_{z}}{\partial x}\\ \frac{\partial A_{y}}{\partial x}-\frac{\partial A_{x}}{\partial y} \end{array} \end{array} \right) \end{eqnarray}
外積のレビチビタ表記(レベル2)
外積はレビチビタ記号を用いて \begin{equation} (\bs{a} \times \bs{b})_{i}=\sum_{jk} \varep_{ijk} a_{j} b_{k} \end{equation} でかける。
レビチビタ記号による表現です。成分表示と違って一行で書けることが利点です。 レビチビタ記号について詳しくはこちらからどうぞ。