スカラー三重積とベクトル三重積
\(\bs{A} \cdot (\bs{B} \times \bs{C})\)の因子をスカラー三重積と呼び、
\(\bs{A} \times (\bs{B} \times \bs{C})\)の因子をベクトル三重積と呼ぶ。
ベクトルを扱う大学物理では、外積や内積に関する公式を使って、計算を進めることが多々あります。 今回は特に重要なスカラー三重積とベクトル三重積の公式について簡単にまとめました。
ちなみに、\(\bs{A} \cdot (\bs{B} \times \bs{C})\)はスカラーで、 \(\bs{A} \times (\bs{B} \times \bs{C})\)はベクトルです。(内積はスカラー、外積はベクトルなので)
外積の持つ性質についてはベクトルの外積を参照してください。
スカラー三重積の公式(レベル1~2)
スカラー三重積について \begin{equation} \label{scalarproduct} \bs{A} \cdot (\bs{B} \times \bs{C})=\bs{B} \cdot (\bs{C} \times \bs{A}) =\bs{C} \cdot (\bs{A} \times \bs{B}) \end{equation} が成り立つ。
有用な公式です。後述する幾何的な意味も合わせて使えるようになりましょう。
証明
真面目に成分で計算する方法と、レビチビタ記号を使う方法の二つで証明します。 (レビチビタ記号について詳しくはこちらから)
(i)成分で計算する方法(レベル1)
\(\bs{A} \cdot (\bs{B} \times \bs{C})=\bs{B} \cdot (\bs{C} \times \bs{A})\)をまず示す。 左辺から計算すると、 \begin{eqnarray} \bs{B} \times \bs{C}=\left( \begin{array}{c} B_{y}C_{z}-B_{z}C_{y} \\ B_{z}C_{x}-B_{x}C_{z}\\ B_{x}C_{y}-B_{y}C_{x} \end{array} \right) \end{eqnarray} より、 \begin{eqnarray} \bs{A} \cdot (\bs{B} \times \bs{C})&=A_{x}(B_{y}C_{z}-B_{z}C_{y}) \nonumber \\ & \quad +A_{y}(B_{z}C_{x}-B_{x}C_{z}) \nonumber \\ & \quad +A_{z}(B_{x}C_{y}-B_{y}C_{x}) \nonumber \\ &=B_{x}(C_{y}A_{z}-C_{z}A_{y}) \nonumber \\ & \quad +B_{y}(C_{z}A_{x}-C_{x}A_{z}) \nonumber \\ & \quad +B_{z}(C_{x}A_{y}-C_{y}A_{x}) \nonumber \\ &=\bs{B} \cdot (\bs{C} \times \bs{A}) \end{eqnarray} となり示せる。全く同様にして、 \(\bs{B} \cdot (\bs{C} \times \bs{A})=\bs{C} \cdot (\bs{A} \times \bs{B})\)も示すことができるので、 以上の二式より、(\ref{scalarproduct})が成り立つことが確認できた。
(ii)レビチビタ記号を使う方法(レベル2)
ベクトルの外積はレビチビタ記号を使って、 \begin{equation} [\bs{A} \times \bs{B}]_{i} = \sum_{jk} \varep_{ijk} A_{j}B{k} \end{equation} と書ける。以下、アインシュタインの規則を使って、和の記号を省略し \begin{equation} \label{outerproduct} [\bs{A} \times \bs{B}]_{i} = \varep_{ijk} A_{j}B{k} \end{equation} と書くことにする。すると、 \begin{eqnarray} \bs{A} \cdot (\bs{B} \times \bs{C})&=A_{i} [\bs{B} \times \bs{C}]_{i} \nonumber \\ &=A_{i} \varepsilon_{ijk} B_{j}C{k} \nonumber \\ &=B_{j} \varepsilon_{jki} C{k}A_{i} \nonumber \\ &=B_{i} \varepsilon_{ijk} C_{j}A_{k} \nonumber \\ &=\bs{B} \cdot (\bs{C} \times \bs{A}) \end{eqnarray} となって\(\bs{A} \cdot (\bs{B} \times \bs{C})=\bs{B} \cdot (\bs{C} \times \bs{A})\)が示せた。 \(\bs{B} \cdot (\bs{C} \times \bs{A})=\bs{C} \cdot (\bs{A} \times \bs{B})\)についても同様。 以上により、(\ref{scalarproduct})が成り立つ。
スカラー三重積には幾何的な意味があり、こちらも重要です。
\(\bs{A} \cdot (\bs{B} \times \bs{C})\)は ベクトル\(\bs{A}\)、\(\bs{B}\)、\(\bs{C}\)を三辺とする、平行六面体の体積に等しい。
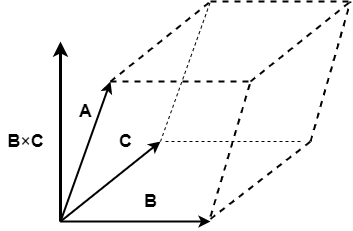
上の図の点線で囲われた六面体の体積が\(\bs{A} \cdot (\bs{B} \times \bs{C})\) になります。この事実を使うと、\(\bs{A} \cdot (\bs{B} \times \bs{C})\)にしろ、 \(\bs{B} \cdot (\bs{C} \times \bs{A})\)にしろ、同じ平行六面体の体積を表していることになるため、 より直感的に式(\ref{scalarproduct})が成り立つことが理解できます。
証明
まず、\((\bs{B} \times \bs{C})\)の大きさは\(\bs{B}\)と\(\bs{C}\)で構成される平行四辺形 (平行六面体の底面)の面積に等しく、\((\bs{B} \times \bs{C})\)の向きはその底面に垂直である。 そして \begin{equation} \label{volume} \bs{A} \cdot (\bs{B} \times \bs{C})=|\bs{B} \times \bs{C}||\bs{A}| \cos \theta \end{equation} であるが、\(|\bs{A}| \cos \theta\)は\(\bs{A}\)のうち\((\bs{B} \times \bs{C})\)の向き に平行な成分であるため、即ち平行六面体の高さを表す。よって、(\ref{volume}) の右辺は底面積と高さの積になっているため、\(\bs{A} \cdot (\bs{B} \times \bs{C})\)は 確かに平行六面体の体積に等しいことが分かった。
ベクトル三重積の公式(レベル1~2)
ベクトル三重積について \begin{equation} \label{vectorproduct} \bs{A} \times (\bs{B} \times \bs{C}) =(\bs{A} \cdot \bs{C}) \bs{B}-(\bs{A} \cdot \bs{B}) \bs{C} \end{equation} が成り立つ。
使う機会はスカラー三重積よりこちらの方が多い気がします。この等式は両辺がベクトルになっている ので、成分で証明するときには三成分それぞれについて示す必要があります。
証明
真面目に成分で計算する方法と、レビチビタ記号を使う方法の二つで証明します。 (レビチビタ記号について詳しくはこちらから)
(i)成分で計算する方法(レベル1)
まずは、左辺の\(x\)成分を計算する。簡単のため、ひとまず\(\bs{D}=\bs{B} \times \bs{C}\)と置いておく。 すると成分を陽にかくと \begin{eqnarray} \bs{A} \times \bs{D}=\left( \begin{array}{c} A_{y}D_{z}-A_{z}D_{y} \\ A_{z}D_{x}-A_{x}D_{z}\\ A_{x}D_{y}-A_{y}D_{x} \end{array} \right) \end{eqnarray} である。よって、\(x\)成分は\([\bs{A} \times \bs{D}]_{x}=A_{y}D_{z}-A_{z}D_{y}\)である。あとは\(\bs{D}=\bs{B} \times \bs{C}\)だったので \(D_{z}\)や\(D_{y}\)に\(\bs{B} \times \bs{C}\)の\(z\)成分、\(y\)成分を代入して計算すると、 \begin{eqnarray} [\bs{A} \times \bs{D}]_{x}&=&A_{y}(B_{x}C_{y}-B_{y}C_{x}) \nonumber \\ & &\quad -A_{z}(B_{z}C_{x}-B_{x}C_{z}) \nonumber \\ &=&(A_{y}C_{y}+A_{z}C_{z})B_{x} \nonumber \\ & &\quad -(A_{z}B_{z}+A_{y}B_{y})C_{x} \nonumber \\ &=&(A_{x}C_{x}+A_{y}C_{y}+A_{z}C_{z})B_{x} \nonumber \\ & &\quad -(A_{z}B_{z}+A_{y}B_{y}+A_{x}B_{x})C_{x} \nonumber \\ &=&(\bs{A} \cdot \bs{C}) B_{x}-(\bs{A} \cdot \bs{B})C_{x} \tag{7} \end{eqnarray} となって確かに成り立っていることが確認できる。ただし、途中、 第一項目で\(A_{x}B_{x}C_{x}\)を勝手に足した後、第二項目で同じ因子を引くことで式変形を行った。
他の成分についても全く同様。
(ii)レビチビタ記号を使う方法(レベル2)
レビチビタ記号を使って外積を \begin{equation} [\bs{A} \times \bs{B}]_{i} = \varep_{ijk} A_{j}B{k} \tag{\ref{outerproduct}} \end{equation} と書くことにする。すると、 \begin{eqnarray} [\bs{A} \times (\bs{B} \times \bs{C})]_{i}&=&\varep_{ijk} A_{j} [\bs{B} \times \bs{C}]_{k} \nonumber \\ &=&\varep_{ijk} A_{j} \varep_{klm} B_{l}C_{m} \nonumber \\ &=&\varep_{ijk} \varep_{klm} A_{j} B_{l}C_{m} \nonumber\\ &=&(\delta_{il} \delta_{jm}- \delta_{im} \delta_{jl}) A_{j} B_{l}C_{m} \nonumber \\ &=&(A_{j} C_{j}) B_{i}-(A_{j}B_{j})C_{i} \nonumber \\ &=&(\bs{A} \cdot \bs{C}) \bs{B}-(\bs{A} \cdot \bs{B}) \bs{C} \end{eqnarray} となって証明は終わる。式変形の途中で、レビチビタ記号とクロネッカーのデルタに関する公式 \begin{equation} \label{Levi-Civitaformula} \varep_{ijk} \varep_{klm}=\delta_{il} \delta_{jm}- \delta_{im} \delta_{jl} \tag{23} \end{equation} を使用した。((\ref{Levi-Civitaformula})の証明はレビチビタ記号を参照。)
一応、成分を使わずに幾何的な性質だけを使って式(\ref{vectorproduct})を導くことも可能ですが、 証明は回りくどくなります。概要だけ以下に置いておきます。
証明(おまけ)(レベル2)
まず、\(\bs{A} \times (\bs{B} \times \bs{C})\) と\((\bs{B} \times \bs{C})\)の内積を取る。これはスカラー三重積の公式(式(\ref{scalarproduct})) より、 \begin{eqnarray} & &(\bs{B} \times \bs{C}) \cdot [\bs{A} \times (\bs{B} \times \bs{C})] \nonumber \\ &=&\bs{A} \cdot [(\bs{B} \times \bs{C}) \times (\bs{B} \times \bs{C})] \nonumber \\ &=&0 \quad (\because 自分自身との外積は0) \end{eqnarray} となって0になる。\((\bs{B} \times \bs{C})\)との外積が0だったので、ベクトル「\(\bs{A} \times (\bs{B} \times \bs{C})\)」 は\(\bs{B}\)と\(\bs{C}\)の張る平面上に存在し、ゆえに \begin{equation} \label{linearcomb} \bs{A} \times (\bs{B} \times \bs{C})=\alpha \bs{B}-\beta \bs{C} \end{equation} と線形結合の形でかける。(ただし、\(\alpha\)や\(\beta\)は展開係数)
続いて\(\boldsymbol{A}\)との内積もとってみる。再びスカラー三重積の公式(式(\ref{scalarproduct}))により、 結果は \begin{eqnarray} \bs{A} \cdot [\bs{A} \times (\bs{B} \times \bs{C})] &=&(\bs{B} \times \bs{C}) \cdot [\bs{A} \times \bs{A}] \nonumber \\ &=&0 \end{eqnarray} となってやはり0になる。この条件を式(\ref{linearcomb})の右辺にもに課す。 \begin{eqnarray} & &\bs{A} \cdot (\alpha \bs{B}-\beta \bs{C})=0 \nonumber \\ & \to & \alpha \bs{A} \cdot \bs{B}=\beta \bs{A} \cdot \bs{C} \nonumber \\ & \to &\frac{\alpha}{\beta}=\frac{\bs{A} \cdot \bs{C}}{\bs{A} \cdot \bs{B}} \end{eqnarray} より、 \begin{eqnarray} \bs{A} \times (\bs{B} \times \bs{C})&=&\gamma (\bs{A} \cdot \bs{C}) \bs{B} \\ &-& \gamma (\bs{A} \cdot \bs{B}) \bs{C} \end{eqnarray} まで変形できる。(ただし、\(\gamma\)は定数)
最後に両辺の大きさを計算して\(\gamma=1\)になることを示す。まず準備として\(\bs{A}\) を線形独立な三つのベクトル、\(\bs{B}\)、\(\bs{C}\)、\(\bs{B} \times \bs{C}\)を使って \begin{eqnarray} \boldsymbol{A}=x \boldsymbol{B}+y \boldsymbol{C} +z (\boldsymbol{B} \times \boldsymbol{C}) \tag{16} \end{eqnarray} をのように分解しておく。これを式(\ref{vectorproduct})に代入する。 \(x\)、\(y\)に比例する項に分けると \begin{eqnarray} \bs{B} \times (\bs{B} \times \bs{C})&=\gamma (\bs{B} \cdot \bs{C}) \bs{B} \nonumber \\ &-\gamma (\bs{B} \cdot \bs{B}) \bs{C} \end{eqnarray} 及び \begin{eqnarray} \bs{C} \times (\bs{B} \times \bs{C})&=\gamma (\bs{C} \cdot \bs{C}) \bs{B} \nonumber \\ &-\gamma (\bs{C} \cdot \bs{B}) \bs{C} \end{eqnarray} のように二つの式に帰着できる。それぞれについて両辺の大きさを取って比べると、 \(\gamma=1\)になることが確認できる。
\begin{eqnarray} \end{eqnarray}