有限の深さの井戸型ポテンシャル
量子力学において以下のようなポテンシャル \begin{equation} \label{potential} V(x) = \begin{cases} V_{0} &(x < -a) \\ 0 &(-a < x < a)\\ V_{0} &(a < x) \end{cases} \end{equation} を有限の深さの井戸型ポテンシャルと呼ぶ。
今回は、以前解いた無限に深い井戸型ポテンシャルの問題の、 深さが有限になった場合を考えましょう。 有限の深さの井戸型ポテンシャルとは、図のように一定範囲でのみ\(0\)で、それ以外\(V_{0}\)のポテンシャルのことです。
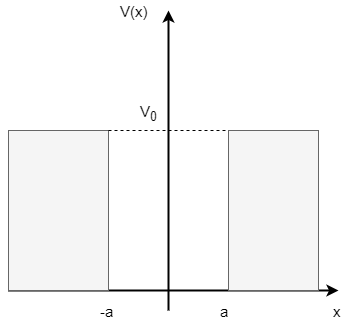
深さが有限になったことで、井戸の外にも波動関数が漏れ出し、深さが無限の場合より 解が複雑になっています。臆することなく、物理的な意味を読み取りましょう。
解の導出(レベル2)
時間依存しないシュレディンガー方程式について、 \(V(x)\)が有限の深さの井戸型ポテンシャル(\ref{potential})式の場合の解を考える。 井戸に束縛された状態、つまり無限遠で\(0\)収束する解にのみ注目すれば、 井戸の中\((-a \leq x \leq a)\)の波動関数は、無限に深い井戸の問題と同様に \begin{eqnarray} \label{innersol} \phi_{n}(x) = \begin{cases} A \sin \left(k_{n} x \right) &(n = 2,4,6...)\\ B \cos \left(k_{n} x \right) &(n = 1,3,5...) \end{cases} \end{eqnarray} である。ただし、\(k_{n}=\sqrt{2mE_{n}}/\hbar\)と置いた。
一方、井戸の外\((x \leq -a, a \leq x)\)では \begin{eqnarray} \label{outersol} \phi_{n}(x) = \begin{cases} \pm C e^{\pm b_{n}x} &(n = 2,4,6...)\\ D e^{-b_{n}|x|} &(n = 1,3,5...) \end{cases} \end{eqnarray} と表される。ただし、\(b_{n}=\sqrt{V_{0}-E_{n}}/\hbar\)と置いた。 また、符号\(\pm\)は、\(a < x \)の側で\(+\)、\(x < -a\)の側で\(-\)を表す。
冒頭でも述べたように、ポテンシャルの壁が有限の高さのため、波動関数の値は 井戸の外でも\(0\)になりません。(無限に深い場合は井戸の外で波動関数の値は\(0\)でした。) これは、量子力学特有の性質であり、物理的な意味については後のセクションで説明します。
導出
方針としては、無限に深い井戸型ポテンシャル と同様に、外と中で問題を分割して考えます。その後、それぞれで得られた解をつなげて答えを得ます。 今回、井戸の中に粒子が存在する場合に興味があるので、\(0 < E < V_{0}\)を仮定しておきます。
初めに、井戸の中について考える。井戸の中ではポテンシャルは\(0\)なので シュレーディンガー方程式は \begin{equation} \label{innerwell} \left( -\frac{\hbar^2}{2m} \frac{d^2}{d x^2} \right) \phi (x)=E \phi (x) \hspace{10pt} (-a < x < a) \end{equation} で表せる。今、 \begin{equation} \label{energy} E = \frac{\hbar^2 k^2}{2m} \end{equation} になるように変数\(k\)を定義する。すなわち \(k:=\sqrt{2mE}/\hbar\)である。すると、(\ref{innerwell})式は \begin{equation} \label{oscillator} \frac{d^2}{d x^2} \phi (x)=-k^2 \phi (x) \hspace{10pt} (-a < x < a) \end{equation} の形に帰着でき、これは単振動の微分方程式になっている。 ゆえに、井戸の中の一般解\(\phi_{in}(x)\)は \begin{equation} \label{insol} \phi_{in}(x) = A \sin kx + B \cos kx \hspace{10pt} (-a < x < a) \end{equation} (\(A,B\)は定数)で与えられる。
続いて、井戸の外の解を考える。井戸の中ではポテンシャルは\(V_{0}\)(定数)なので シュレーディンガー方程式は \begin{equation} \label{outerwell} \left( -\frac{\hbar^2}{2m} \frac{d^2}{d x^2} + V_{0}\right) \phi (x)=E \phi (x) \hspace{10pt} (x \leq -a, a \leq x) \end{equation} で表せる。今、 \begin{equation} \label{bdef} V_{0}-E = \frac{\hbar^2 b^2}{2m} \end{equation} になるように変数\(b\)を定義する。すなわち \(b:=\sqrt{2mV_{0}-E}/\hbar\)である。すると、井戸の中の場合と同じように \begin{equation} \phi_{out}(x) = Ce^{bx}+D e^{-bx} \hspace{10pt} (x \leq -a, a \leq x) \end{equation} で与えられる。ただし、\(E < V_{0}\)を仮定した。
さらに、\(x \to \infty\)及び\(x \to -\infty\)でそれぞれ発散しない (つまり、波動関数が井戸の中で束縛されている)条件を課すと \begin{equation} \label{outsol} \phi_{out}(x) = \begin{cases} Ce^{bx} \hspace{10pt} (x \leq -a) \\ D e^{-bx} \hspace{10pt} (a \leq x) \end{cases} \end{equation} のように解の形が限定できる。
あとは無限に深い井戸型ポテンシャルの問題のときと同様に、境界条件を考えて まだ決まっていない定数\(A,B,k,C,D,b\)を決定していけばよい。
さて、井戸の中の解\(\phi_{in}(x)\)と、井戸の外の解\(\phi_{out}(x)\)が 連続かつ滑らかであることを要求する。つまり境界条件として\(x=\pm a\)でそれぞれ \begin{eqnarray} \label{bound1} \begin{cases} \phi_{in}(\pm a) = \phi_{out}(\pm a) \\ \frac{d \phi_{in}}{dx}(\pm a) = \frac{d \phi_{out}}{dx}(\pm a) \end{cases} \end{eqnarray} を課す。井戸が無限に深かった場合とは異なり、波動関数の微分にも条件がかかっていることに 注意しよう。波動関数の微分は運動量に対応\(\hat{p}=i\pdiff{}{dx}\)するから、 これは\(x=\pm a\)で運動量が一致する条件として解釈できる。
一度に\(x=\pm a\)を扱うと混乱を招くので、いったん\(x=a\)の条件から処理しよう。 (\ref{bound1})式に、\(\phi_{in}(a),\phi_{out}(a)\)の値を代入。 \begin{eqnarray} \begin{cases} A \sin ka + B \cos ka = D e^{-ba} \\ Ak \cos ka - Bk \sin ka = - Db e^{-ba} \end{cases} \end{eqnarray} つづいて、\(x=-a\)では、次の通りである。 \begin{eqnarray} \begin{cases} -A \sin ka + B \cos ka = C e^{-ba} \\ Ak \cos ka + Bk \sin ka = Cb e^{-ba} \end{cases} \end{eqnarray} (微分した後に\(x=-a\)を代入しないと符号ミスを起こすので注意せよ)
ここで、連続条件を足し合わせると、 \begin{equation} 2B \cos ka = D e^{-ba}+C e^{-ba} \end{equation} であるが、もし、\(B=0\)ならば、\(C=-D\)でなければ等式が成立しないことがわかる。 まったく同様に、滑らかな条件を足し合わせると、 \begin{equation} 2Ak \cos ka = -Db e^{-ba}+Cb e^{-ba} \end{equation} であるが、\(A=0\)ならば、\(C=D\)でなければ等式が成立しないことがわかる。 自明な解\(A=B=C=D=0\)を除けば、\(C=D\)と\(C=-D\)は両立しないのだから、 以上の考察から(1)\(A \neq 0, B=0\)かつ\(C=-D\)の場合と、(2)\(A = 0, B \neq 0\)かつ\(C=D\)の場合 に分けて考えればよい。
(1)\(B=0\)の場合
この場合、\(C=-D\)なのだから、解は \begin{equation} \phi(x) = \begin{cases} C e^{bx} \hspace{10pt} (x \leq -a) \\ A \sin kx \hspace{10pt} (-a < x < a) \\ -C e^{-bx} \hspace{10pt} (a \leq x) \end{cases} \end{equation} であらわされる。ここで、\(x= a\)における連続の条件、および滑らかな条件をもう一度考えると、 \begin{eqnarray} A \sin ka = -C e^{-bx} \\ Ak \cos ka = Cb e^{-bx} \end{eqnarray} この二つの式を辺々割り算すると、 \begin{eqnarray} k \cot ka = -b \end{eqnarray} を得る。一方、 \(k=\sqrt{2mE}/\hbar,b=\sqrt{2mV_{0}-E}/\hbar\)だったから、\(k,b\)の間には関係式 \begin{eqnarray} k^2 + b^2 = \frac{2mV_{0}}{\hbar^2} \end{eqnarray} が成り立つ。これらの式は、\(\xi = ka,\eta=ba\)と置くと \begin{eqnarray} \label{eveneq} &&\eta = -\xi \cot \xi\\ &&\xi^2 + \eta^2 = \frac{2mV_{0}a^2}{\hbar^2} \end{eqnarray} のように、\(\xi,\eta\)のみの連立方程式に帰着でき、これを 解けば\(k,b\)を求めることができる。
しかし、残念なことにこの連立方程式(\ref{eveneq})は、解析的に解くことはできない。 ただし、(\ref{eveneq})式を、解の個数を数える問題として見ることで、定性的な性質は理解できる。 ここに、\(k=\sqrt{2mE}/\hbar,b=\sqrt{2mV_{0}-E}/\hbar\)なので、考える範囲は\(\xi > 0, \eta >0\)でよい。
例えば、円\(\xi^2 + \eta^2 = \frac{2mV_{0}a^2}{\hbar^2}\)の半径\(\frac{a}{\hbar}\sqrt{2mV_{0}}\) が\(\frac{\pi}{2}\)より小さいとき \begin{eqnarray} \label{lessthanpiovertwo} \frac{a}{\hbar}\sqrt{2mV_{0}} < \frac{\pi}{2} \end{eqnarray} 連立方程式(\ref{eveneq})は解をもたない。これはグラフを書いて 交点の数を数えれば明らかである。同様に、 \begin{eqnarray} \frac{\pi}{2} \leq \frac{a}{\hbar}\sqrt{2mV_{0}} < \frac{3\pi}{2} \end{eqnarray} の時は一つ解が存在し、 \begin{eqnarray} \frac{(2n-1)\pi}{2} \leq \frac{a}{\hbar}\sqrt{2mV_{0}} < \frac{(2n+1)\pi}{2} \end{eqnarray} の時、解は\(n\)個存在する。これは\(k,b\)の解の個数の話だったから、これはすなわち \(k,b\)が\(n\)でラベル付けできることを意味し(\(k=k_{n},b=b_{n}\))、それに応じて 解も\(n\)でラベル付けされる。
(2)\(A=0\)の場合
この場合、\(C=D\)なのだから、解は \begin{equation} \phi(x) = \begin{cases} B \cos kx \hspace{10pt} (-a < x < a) \\ C e^{-b|x|} \hspace{10pt} (x \leq -a, a \leq x) \end{cases} \end{equation} であらわされる。\(x= a\)における連続の条件、および滑らかな条件をもう一度考えると、 \begin{eqnarray} B \cos ka = -C e^{-bx} \\ Bk \sin ka = Cb e^{-bx} \end{eqnarray} となるから、この二つを辺々割り算すると、 \begin{eqnarray} k \tan ka = b \end{eqnarray} \(k,b\)の間には関係式 \begin{eqnarray} k^2 + b^2 = \frac{2mV_{0}}{\hbar^2} \end{eqnarray} が成り立つ。以上の式を、\(\xi = ka,\eta=ba\)で書くと、 \begin{eqnarray} \label{oddeq} &&\eta = \xi \tan \xi\\ &&\xi^2 + \eta^2 = \frac{2mV_{0}a^2}{\hbar^2} \end{eqnarray} を得る。あとは、(1)\(B=0\)の場合と同じく、解の個数を数える問題を考えていこう。
今回の場合も、グラフを書いて交点を数えていけば、 \begin{eqnarray} \frac{a}{\hbar}\sqrt{2mV_{0}} < \pi \end{eqnarray} の時、(\ref{oddeq})には一つ解が存在し、同様に、 \begin{eqnarray} \pi \leq \frac{a}{\hbar}\sqrt{2mV_{0}} < 2\pi \end{eqnarray} の時は解が二つ、 \begin{eqnarray} (n'-1)\pi \leq \frac{a}{\hbar}\sqrt{2mV_{0}} < n' \pi \end{eqnarray} の時、解は\(n'\)個存在する。\(k,b\)が\(n'\)でラベル付けできることを意味し(\(k=k_{n'},b=b_{n'}\))、それに応じて 解も\(n'\)でラベル付けされる。
最後に(1)\(B=0\)の場合と、(2)\(A=0\)の場合を統合し、(\ref{innersol},\ref{outersol})式 を得る。
物理的な解釈(レベル2)
有限の深さの井戸型ポテンシャル(\ref{potential})式の元でのシュレーディンガー方程式の解は 整数\(n\)でラベル付けされる。また、各状態に対応するエネルギーも\(n\)でラベル付けされ、 \begin{eqnarray} E = \frac{\hbar k_{n}^2}{2m} \end{eqnarray} である。つまり、エネルギーは量子化されている。
無限に深い井戸型ポテンシャルの時と同じように、井戸に束縛された解(\ref{innersol},\ref{outersol})式 のエネルギーは量子化されています。また、その値は井戸型ポテンシャルの幅\(a\)だけでなく、井戸の深さ\(V_{0}\) にも依存します。
井戸に束縛された解(\ref{innersol},\ref{outersol})式の中で、最もエネルギー が低い状態(基底状態)は \begin{equation} \label{groundstate} \phi(x) = \begin{cases} B \cos k_{1}x \hspace{10pt} (-a < x < a) \\ C e^{-b_{1}|x|} \hspace{10pt} (x \leq -a, a \leq x) \end{cases} \end{equation} 基底状態の次にエネルギーが低い状態(第一励起)は \begin{equation} \label{1stexcitestate} \phi(x) = \begin{cases} C e^{b_{2}x} \hspace{10pt} (x \leq -a) \\ A \sin k_{2}x \hspace{10pt} (-a < x < a) \\ -C e^{-b_{2}x} \hspace{10pt} (a \leq x) \end{cases} \end{equation} である。
井戸の深さ\(V_{0}\)を浅くしていったとき、エネルギーが高い状態から次々と井戸溢れていってしまいますが、 (\ref{groundstate})式の解は最後まで井戸に残り続けます。つまり、エネルギーが一番低い状態(基底状態)ということです。
実際\(V_{0} \to 0\)でも、 (\ref{groundstate})式の解が存在する条件 \begin{eqnarray} \frac{a}{\hbar}\sqrt{2mV_{0}} < \frac{\pi}{2} \tag{\ref{lessthanpiovertwo}} \end{eqnarray} は成り立ちます。基底状態が井戸の中で\(\cos k x\)と振る舞うのは、井戸が無限に深い場合と同様ですね。
基底状態の次にエネルギーが低い状態(第一励起状態)は(\ref{1stexcitestate})式で与えられます。 無限に深い場合と同じく、井戸の中では\(\sin k x\)として振る舞います。
無限に深い場合との違いと比較(レベル2)
有限の深さの井戸型ポテンシャルにおける、束縛状態は(\ref{innersol},\ref{outersol})式 で与えられる。無限に深い場合と異なり、井戸の外でも有限の値を持つ。
無限に深い井戸の場合、井戸の外の波動関数は\(0\)でした。井戸の深さが有限の場合は、僅かながら 井戸の外でも値を持ちます。
これは量子論特有の効果です。古典論では、エネルギーがポテンシャルより低い場合、粒子はその場所に 安定して存在できませが、物質波は、後の記事で指摘するように不確定性原理の関係でわずかながら染み出すことができます。 ただし、その効果は \begin{eqnarray} &&e^{-bx} \hspace{10pt} (a \leq x) \nonumber \\ &&= e^{-\sqrt{2mV_{0}-E}/\hbar} \nonumber \\ &&\tolim{V_{0}/\hbar}{\infty} 0 \end{eqnarray} であるため、ポテンシャルが深い場合\(V_{0} \to \infty\)、 または(ポテンシャルと比較して)量子効果が無視できる場合\(\hbar \to 0\)、染み出しの効果は無視できます。
有限の深さの井戸型ポテンシャルにおける解 \begin{eqnarray} \phi_{in;n}(x) = \begin{cases} A \sin \left(k_{n} x \right) &(n = 2,4,6...)\\ B \cos \left(k_{n} x \right) &(n = 1,3,5...) \end{cases} \end{eqnarray} \begin{eqnarray} \phi_{out;n}(x) = \begin{cases} \pm C e^{\pm b_{n}x} &(n = 2,4,6...)\\ D e^{-b_{n}|x|} &(n = 1,3,5...) \end{cases} \end{eqnarray} は、\(a\)を固定したもとで極限\(V_{0} \to \infty\)をとると、無限に深い井戸型ポテンシャルのの解 \begin{eqnarray} \phi_{in;n}(x) = \begin{cases} \sqrt{\frac{1}{a}} \sin \left(\frac{n \pi}{2a} x \right) &(n = 2,4,6...)\\ \sqrt{\frac{1}{a}} \cos \left(\frac{n \pi}{2a} x \right) &(n = 1,3,5...) \end{cases} \end{eqnarray} \begin{eqnarray} \phi_{out;n}(x) = 0 \ \hspace{10pt} ( n = 1,2,3,4,,, ) \end{eqnarray} に帰着される。
当然といえば当然ですが、今回導いた解(\ref{innersol},\ref{outersol})式 で\(V_{0} \to \infty\)の極限をとると、無限に深い井戸の場合の解 に帰着されます。井戸の深さが有限の時は解の個数が\(V_{0}\)によって 決まっていましたが、 \begin{eqnarray} &&\frac{(2n-1)\pi}{2} \leq \frac{a}{\hbar}\sqrt{2mV_{0}} < \frac{(2n+1)\pi}{2} \hspace{10pt} (\sin k_{n}x型 の解の個数)\\ &&(n'-1)\pi \leq \frac{a}{\hbar}\sqrt{2mV_{0}} < n' \pi \hspace{10pt} (\cos k_{n'}x 型の解の個数) \end{eqnarray} この二つは変形すると \begin{eqnarray} &&\frac{\left(n-\frac{1}{2} \right)^2 h^2}{8m} \leq V_{0}a^2 < \frac{\left(n+\frac{1}{2} \right)^2 h^2}{8m} \hspace{10pt} (\sin k_{n}x型 の解の個数)\\ &&\frac{(n'-1)^2 h^2}{8m} \leq V_{0}a^2 < \frac{n'^2 h^2}{8m} \hspace{10pt} (\cos k_{n'}x 型の解の個数) \end{eqnarray} であるため、\(a\)を固定した状態で\(V_{0} \to \infty\)の極限をとると、解の個数\(n+n'\)も無限になること がわかります。