オームの法則
定常電流密度\(\bs{j}(\bs{r})\)、静電場\(\bs{E}(\bs{r})\)について以下が成り立つ。 \begin{equation} \label{Ohm} \bs{j}(\bs{r})=\sigma \bs{E}(\bs{r}) \end{equation} これを微分型(微分形)のオームの法則と呼ぶ。 (ただし\(\sigma\)は電気伝導度)
有名なオームの法則です。よく知られているのは上記の微分形ではなく、下に示す 積分形だと思いますが、大学物理で使うのはこちらです。また、上述の定常電流や静電場とは、 時間で変化しない電流、電場のことです。 オームの法則について簡単に まとめました。
積分形(レベル1)
定常電流\(I\)と電圧\(V\)について以下が成り立つ。 \begin{equation} \label{intOhm} V=RI \end{equation} これを積分型(積分形)のオームの法則と呼ぶ。 (ただし\(R\)は抵抗)
中学で習うこのオームの法則は積分形で書かれています。実際、\(V\)や\(I\)は積分を使って書き換える ことができます。(詳しくは→電流密度、電圧の記事参照。)
\begin{eqnarray} \label{voltage} V&=&\int_{C} \bs{E}(\bs{r}) \cdot d \bs{l} \\ \label{current} I&=&\int_{S} \bs{j}(\bs{r}) \cdot \bs{n}(\bs{r}) dS \\ \end{eqnarray}微分形と積分形は見た目が大きく異なりますが、両者は同じことを言っています。積分形から微分形への 導出は下のギモンを参考にしてください。微分形の意義や必要性に ついてはこちらの記事を参照。
ちなみに、現実の回路で使うのはこちらではなく、電源による起電力を考慮に 入れた表式です。詳しくは下のギモンを参照。
法則の意味(レベル1)
オームの法則は、導線にかかる電場(電圧)と電流密度(電流) が比例するという関係式。
オームの法則は、回路の実験をしたことがあるなら直感的に理解できると思います。 すなわち、電圧(電場)をかければかけるほど流れる電流(電流密度)は多くなるということです。
続いて積分形、微分形の比例係数に注目してみましょう。\(R\)と\(\sigma\)に ついて物理的な意味は以下の通りです。
積分形(\ref{intOhm})式の比例係数\(R\)は抵抗であり、 電流の流れにくさを表す。反対に微分形(\ref{Ohm})式の 比例係数\(\sigma\)は電気伝導度であり、電流の流れやすさを表す。
後述するように、両者の係数は反比例の関係\(R \propto {1 \over \sigma}\)に あり、意味も反転しているので注意してください。ここでは\(R\)と\(\sigma\)の関係と それぞれの意味について補足します。
まず、抵抗\(R\)についてですが、一般に断面積が同じ導線なら長さが長いほど 抵抗は大きく、また、長さが同じなら断面積が広いほど抵抗は小さくなるという性質があります。 より厳密にいうと、抵抗は導線の長さに比例し、断面積に反比例します。これを数式でかくと \begin{equation} \label{resistance} R=\rho \frac{l}{S} \end{equation} のようになります。ここに\(\rho\)は抵抗率というパラメータで、導線の材質にのみ依存します。 (長さや太さに依存しない)つまり、その物質がどれだけ電流が流れにくいかを示しています。
ここで、抵抗率\(\rho\)の逆数として\(\sigma\)を定義します。 \begin{eqnarray} \label{conductivity} \sigma = \frac{1}{\rho} \end{eqnarray} ここで導入された\(\sigma\)は電気伝導度と呼ばれるパラメータで、 抵抗率とは逆に、どれだけ電流が流れやすいがを表しています。
法則の導出(レベル1)
ここではよく知られたオームの法則の積分形(\ref{intOhm})式から出発して 微分形(\ref{Ohm})式を導きます。
導出
断面積\(S\)が一定の導線について、点\(A\)から点\(B\)へ流れる電流を考える。 まずは簡単のため、電流は\(x\)軸に平行に流れているとする。 オームの法則の積分形により、この電流と点\(A,B\)間にかかっている電圧について以下が成り立つ。
\begin{equation} V=RI \tag{\ref{intOhm}} \end{equation}今、点\(A,B\)間が微小であり、距離が\(\Delta l\)の場合を考える。 この場合、(\ref{resistance})式より \begin{equation} R={\rho \over S}\Delta l \end{equation} が成り立つ。一方、電圧は(\ref{voltage})式より、電流が\(x\)軸に平行という仮定から \begin{eqnarray} V&=&\int_{C} \bs{E}(\bs{r}) \cdot d \bs{l} \\ &=& \int_{x_{A}}^{x_{B}} E_{x}(\bs{r}) dx \end{eqnarray} である。(ただし、積分経路\(C\)は点\(A,B\)を結ぶ電流に沿った経路で、 \(x_{A},x_{B}\)はそれぞれ点\(A,B\)の\(x\)座標。)
ここで点\(B\)が点\(A\)より\(\Delta l\)だけ下流側にあるので \(x_{B}=x_{A}+\Delta l\)である。ゆえに、 \begin{eqnarray} V&=&\int_{x_{A}}^{x_{B}} E_{x}(\bs{r}) dx \\ &=&\int_{x_{A}}^{x_{A}+\Delta l} E_{x}(\bs{r}) dx \\ &=& E_{x}(\bs{r}) \Delta l +O(\Delta l^2) \end{eqnarray} である。(途中、\(\Delta l\)が十分小さいとして 積分中のテイラー展開を使った。)
最後に電流については、電流が\(x\)に平行という仮定と(\ref{current})式から \begin{eqnarray} I&=& \int_{S} \bs{j}(\bs{r}) \cdot \bs{n}(\bs{r}) dS \\ &=& \int_{S} j_{x}(\bs{r}) dS \\ &=& j_{x}(\bs{r}) S \end{eqnarray} を得る。ただし、最後の行で\(S\)が十分小さいことを仮定した。
以上の抵抗、電圧、電流の表式を(\ref{intOhm})式に適用する。
\begin{equation} E_{x}(\bs{r}) \Delta l+O(\Delta l^2)={\rho \over S}\Delta l j_{x}(\bs{r}) S \end{equation}これを両辺\(\Delta l\)で割って\(\Delta l \to 0\)を取ると \begin{equation} E_{x}(\bs{r}) = \rho j_{x}(\bs{r}) \end{equation} となり、 他の成分についても同様に言えるので 結論として \begin{equation} \bs{j}(\bs{r})=\sigma \bs{E}(\bs{r}) \tag{\ref{Ohm}} \end{equation} が得られる。(ただし、最後に \(\sigma={1 \over \rho}\)を使った。)
ちなみに、この導出ですが、回路を考える上で重要な起電力の存在を考慮に入れていません。 起電力まで含んだ表式は下のギモンを見てください。
起電力を含む場合(レベル2)
静電力は保存力なので \begin{equation} \label{oint0} \oint_{C} \bs{E}(\bs{r}) \cdot d\bs{l}=0 \end{equation} であるが、(\ref{voltage})式よりこれは一周する回路では \(V=0\)を表す。これをそのまま(\ref{intOhm})式に代入すると、 \begin{equation} 0=RI \end{equation} となって明らかにこの式は現実では成り立っていない。
静電場の渦なしの法則の記事でも述べたように、静電力は保存力であり、 ポテンシャルに対応する電位を定義できます。しかし、この電位は一周するともとの値に戻る性質を 持っているのでした。
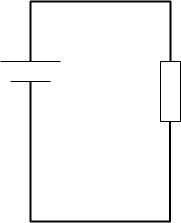
なので、例えば図1のような回路を考えたとき、一周すると電位 はもとに戻るのでその差(つまりは電圧)は自明に\(0\)なはずです。けれどこれを そのままオームの法則へ代入すると、電流は流れていても電流は\(0\)というおかしな 結論が得られてしまいます。
この矛盾は電源(電池)の持つ起電力を考慮することで回避できます。
定常電流密度\(\bs{j}(\bs{r})\)、静電場\(\bs{E}(\bs{r})\)、及び 電源による非保存的な電場\(\bs{E}_{ex}(\bs{r})\)について以下が成り立つ。 \begin{equation} \label{Ohm2} \bs{j}(\bs{r})=\sigma (\bs{E}(\bs{r})+\bs{E}_{ex}(\bs{r})) \end{equation} また、同様に二点間を流れる定常電流\(I\)とその間の電圧\(V\)、 及びその間に含まれる起電力\(V_{ex}\)について以下が成り立つ。 \begin{equation} V_{ex}+V=RI \end{equation} 特に一周する経路では\(V=0\)なので \begin{equation} V_{ex}=RI \end{equation} である。(\(V_{ex} \neq 0\)である)
起電力を含めるようにオームの法則(\ref{Ohm})式を拡張したのが(\ref{Ohm2})式です。 ここで導入された非保存的な電場\(\bs{E}_{ex}(\bs{r})\)は静電場と違い、保存力ではない ので周回積分しても\(0\)になりません。
電源(電池)を跨がない経路を考える場合は最初に紹介した \begin{equation} V=RI \tag{\ref{intOhm}} \end{equation} が使えます。高校以前では起電力と電位差をまとめて電圧と呼んでいたので この表式だったわけですね。
オームの法則(\ref{Ohm})式を積分するときは、電池や電源が積分する経路に入っていないか気を付けましょう。