定常電流の保存則
定常電流密度\(\bs{j}(\bs{r})\)について以下が成り立つ。 \begin{equation} \label{currentconservation} \nabla \cdot \bs{j}(\bs{r})=0 \end{equation} これを微分型(微分形)の定常電流の保存則と呼ぶ。
定常電流とは時間で変化しない電流のことです。電流密度の定義や意味については 電流密度の記事からどうぞ。定常電流の保存則について簡単に まとめました。
積分形(レベル1)
定常電流密度\(\bs{j}(\bs{r})\)について以下が成り立つ。
\begin{equation}
\label{intcurrentconservation}
\int_{S} \bs{j}(\bs{r}) \cdot \bs{n}(\bs{r}) dS=0
\end{equation}
(ただし、Sは3次元領域の表面全体)
これを積分型(積分形)の定常電流の保存則と呼ぶ。
微分形と積分形は見た目が大きく異なりますが、両者は同じことを言っています。積分形から微分形への 導出は下のギモンを参考にしてください。微分形の意義や必要性に ついてはこちらの記事を参照。
後述するように、よくある間違いとして、電流と電流密度の関係式 \begin{equation} \label{currentdens} I=\int_{S} \bs{j}(\bs{r},t) \cdot \bs{n}(\bs{r}) dS \end{equation} と積分形の保存則(\ref{intcurrentconservation})式を混同してしまうことがありますが 両者の積分範囲\(S\)には(同じ記号を使っていますが)以下のような違いがあります。
(\ref{currentdens})式の積分領域は ある3次元領域の断面(開曲面)である。 一方(\ref{intcurrentconservation})式の積分範囲は 3次元領域の表面全体(閉曲面)である。
要は縁のある断面か、全体を覆う面全体かの違いです。紛らわしいですが重要な差異なので 気を付けましょう。
法則の意味(レベル1)
定常電流の保存則(\ref{currentconservation})式の意味は文字通り定常電流の保存、 即ち、定常電流は勝手に発生・消滅しないことを表す。
発散の意味がベクトルの湧き出しであることを理解していれば(\ref{currentconservation})式
の意味が電流密度の湧き出しが\(0\)、即ち勝手に定常電流が発生したり消滅したりしないという意味だと理解できます。
(ベクトルの発散について詳しくはこちらから。)
あるいは、(\ref{currentconservation})式だとイメージがしにくい場合には、(\ref{intcurrentconservation})式 を見てみると、表面\(S\)全体を通した流入流出量の総和が\(0\)、つまり、ある領域に入ってきた分だけ出ていっている ということを表しています。これは勝手に電流が増えないことを示しています。
法則の導出(レベル1)
ここではまず、導出が簡単な積分形(\ref{intcurrentconservation})式を導いた後、 ガウスの定理を使って微分形(\ref{currentconservation})式 を導きます。(ガウスの定理について詳しくは→こちらから)
導出
まず、以下の図1のような導線の断片を模した仮想的な円柱を考え、そこを通過する定常電流を考えます。 この電流は時間によらないので、円柱の片方の底面 から入ってきた分だけ、もう片方の面から電流は出ていくはずです。
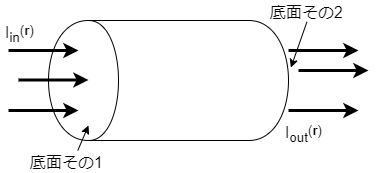
それはつまり、円柱に入ってくる電流を\(I_{in}\)、出ていく電流を\(I_{out}\) とした時、 \begin{equation} I_{in}=I_{out} \end{equation} ということです。
さて、便利のため、電流が入ってくる面を底面その\(1\)、出ていく面を底面その\(2\) と呼ぶことにします。そして、図2のように底面その\(1,2\)に垂直な単位ベクトルを\(\bs{n}_{in},\bs{n}_{out}\) とし、側面についても同様に\(\bs{n}_{around}\)を定めます。
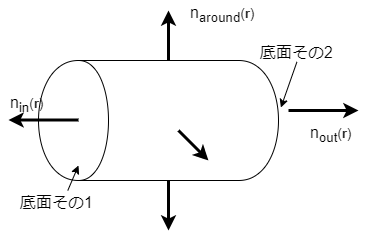
ここで、\(\bs{n}\)は全て円柱に対して外向きに取ったので\(\bs{n}_{in}\) の向きが電流が入ってくる向きとは反転していることに注意してください。
今、導線の側面から出入りする電流はないので\(I_{around}=0\)です。 これは電流密度の表式(\ref{currentdens})を使って書くと \begin{eqnarray} I_{around}&=&\int_{円柱の側面} \bs{j}(\bs{r},t) \cdot \bs{n}_{around}(\bs{r}) dS \nonumber \\ &=&0 \end{eqnarray} となります。
さて、\(I_{out}-I_{in}=0\)、\(I_{around}=0\)より、\(I_{out}-I_{in}+I_{around}=0\)が成り立ちます。 ここで\(I_{out},I_{in}\)を電流密度の表式で書くと、 \begin{equation} I_{out}=\int_{底面その2} \bs{j}(\bs{r},t) \cdot \bs{n}_{out}(\bs{r}) dS \end{equation} \begin{eqnarray} I_{in}&=&\int_{底面その1} \bs{j}(\bs{r},t) \cdot -\bs{n}_{in}(\bs{r}) dS \nonumber \\ &=&-\int_{底面その1} \bs{j}(\bs{r},t) \cdot \bs{n}_{in}(\bs{r}) dS \end{eqnarray} (上でも述べましたが\(\bs{n}_{in}\)と電流が入ってくる向きが正反対なので、\(I_{in}\) の表式の中にマイナスがついていることに注意してください。) のように書けますが、\(I_{out}-I_{in}+I_{around}=0\)にこれらを代入すると \begin{eqnarray} 0&=&I_{out}-I_{in}+I_{around} \nonumber \\ &=& \int_{底面その2} \bs{j}(\bs{r},t) \cdot \bs{n}_{out}(\bs{r}) dS \nonumber \\ & & \ +\int_{底面その1} \bs{j}(\bs{r},t) \cdot \bs{n}_{in}(\bs{r}) dS \nonumber \\ & & \ +\int_{円柱の側面} \bs{j}(\bs{r},t) \cdot \bs{n}_{around}(\bs{r}) dS \nonumber \\ &=& \int_{円柱の表面全体} \bs{j}(\bs{r},t) \cdot \bs{n}(\bs{r}) dS \end{eqnarray} より、導線を模した図1,図2のような円柱について \begin{equation} \int_{S} \bs{j}(\bs{r}) \cdot \bs{n}(\bs{r}) dS=0 \tag{\ref{intcurrentconservation}} \end{equation} が成り立つと分かる。以上の議論は円柱に限らず同様に成り立つ。ゆえに定常電流の保存則の積分形 (\ref{intcurrentconservation})式が導出できた。
続いてこの積分形から微分形(\ref{currentconservation})を導出する。これは ガウスの定理 \begin{equation} \label{Gausstheorem} \int_{V}\nabla \cdot \bs{V}(\bs{r}) \mathrm dV =\int_{S} \bs{V}(\bs{r}) \cdot \bs{n}(\bs{r}) \mathrm dS \end{equation} (\ref{intcurrentconservation})式にを使えば \begin{equation} \int_{V}\nabla \cdot \bs{j}(\bs{r}) \mathrm dV =0 \end{equation} であって、これはすなわち \begin{equation} \nabla \cdot \bs{j}(\bs{r})=0 \tag{\ref{currentconservation}} \end{equation} を表す。