ケプラーの第2法則
太陽と惑星を結ぶ動径に関して、その面積速度は常に一定。
ケプラーの法則の二つ目です。最初にケプラーが発見したのはこの第2法則といわれています。 この法則について要点を簡単まとめました。
面積速度の定義(レベル1)
面積速度とは単位時間あたりの惑星が掃く面積の変化であり、式でかくと \begin{equation} V_{s}=\frac{dS}{dt} \end{equation} で表される。
法則について理解するために、まずは面積速度とは何かを押さえておきましょう。 普通の速度は\(v=\frac{dx}{dt}\)と変位の時間微分でしたが、面積速度は面積の時間微分になっています。 これが速いほど、1秒あたりに惑星が掃く面積が広いことになります。
ここで、惑星が掃く面積とは以下の例のように惑星が動いた軌跡と、二つの位置ベクトルを 三辺とする三角形の面積(灰色の部分)のことです。
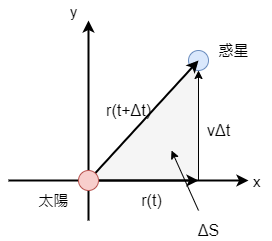
上図では、円運動の場合を示しているため、直角三角形になっていますが、一般にはそうであるあるとは 限りません。
円運動の場合は簡単に面積速度の計算ができます。底辺が\(r\)、 高さが\(v \Delta t=r \dot{\theta} \Delta t\) (円運動の速度の公式)より、\(\Delta S=\frac{1}{2} r^2 \dot{\theta} \Delta t\)なので \begin{equation} V_{s}=\frac{1}{2}r^2 \dot{\theta} \end{equation} となります。
導出(レベル1)
第2法則もまた、万有引力の法則からの帰結として導くことができます。 今回は二つの方法で第2法則を導いてみます。
惑星の軌道が楕円の時、面積速度は \begin{equation} \label{areavelocity} V_{s}=\frac{1}{2}r^2 \dot{\theta} \end{equation} で表される。そして、万有引力の下ではこの量は保存する。 即ち \begin{equation} \label{conservation} \frac{d V_{s}}{dt}=0 \end{equation}
導出方法の一つ目です。普通はこちらを使って導出します。 以下では前半で(\ref{areavelocity})式を示し、後半で(\ref{conservation})式 が得られることを確認します。
導出
軌道が楕円の時、惑星が掃く面積は以下の図のようになる。
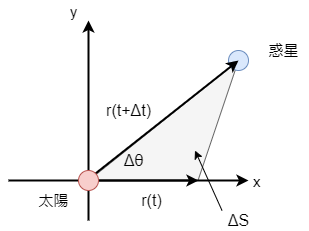
さて、\(\bs{r}(t)\)と\(\bs{r}(t+\Delta t)\)を二辺とし、その間の 角度が\(\Delta \theta\)の三角形の面積は \begin{equation} \Delta S=\frac{1}{2}|\bs{r}(t)||\bs{r}(t+\Delta t)|\sin \Delta \theta \end{equation} でかける。ここで\(\Delta \theta\)が十分小さければ、 \(\sin \Delta \theta \simeq \Delta \theta\)である。また \(\bs{r}(t+\Delta t) \simeq \bs{r}(t)+\bs{r}'(t) \Delta t\)より \begin{equation} \frac{\Delta S}{\Delta t} \simeq \frac{1}{2}|\bs{r}(t)|^2 \frac{\Delta \theta}{\Delta t} \end{equation} であり、\(\Delta t \to 0\)を取ると、 \begin{equation} V_{s}=\frac{1}{2}r^2 \dot{\theta} \tag{\ref{areavelocity}} \end{equation} を得る。
続いてこの量が時間に依らないことを示す。
これは万有引力の運動方程式の\(\theta\)成分
(運動方程式は万有引力の法則にも記載してます。)
\begin{equation}
m \frac{1}{r} \frac{d}{d t}(r^2 \dot{\theta} )=0
\end{equation}
から速やかに
\begin{equation}
\frac{d}{d t}(r^2 \dot{\theta} )=0
\end{equation}
即ち
\begin{equation}
\frac{d V_{s}}{dt}=0 \tag{\ref{conservation}}
\end{equation}
が求まる。
惑星の軌道が楕円の時、面積速度は \begin{equation} \label{areavelocity2} V_{s}=\frac{1}{2}|\bs{r}(t) \times \bs{v}(t)| \end{equation} とも表せる。そして、万有引力の下ではこの量は保存する。
面積速度のベクトルを使った別表現です。上と同じように、(\ref{areavelocity2})式 を示した後、これが時間に依らないことをいいます。導出としてはこちらの方が 難易度は高いです。
導出
まず、図2の三角形の面積は \begin{equation} \Delta S=\frac{1}{2}|\bs{r}(t)||\bs{r}(t+\Delta t)|\sin \Delta \theta \end{equation} とかけるが、これは外積を使うと \begin{equation} \Delta S=\frac{1}{2}|\bs{r}(t) \times \bs{r}(t+\Delta t)| \end{equation} と表せる。 (外積について詳しくは→外積とその諸性質 参照)
ここで、\(|\bs{r}(t) \times \bs{r}(t)|=0\)(自分自身との外積は\(0\)) より \begin{equation} \Delta S=\frac{1}{2}|\bs{r}(t) \times (\bs{r}(t+\Delta t)-\bs{r}(t))| \end{equation} 両辺\(\Delta t\)で割って、\(\Delta t \to 0\)を取ると、 \begin{equation} V_{s}=\frac{1}{2}|\bs{r}(t) \times \bs{v}(t)| \tag{\ref{areavelocity2}} \end{equation} を得る。
続いてこれが保存することを示す。今、万有引力では角運動量
\(\bs{L}=m(\bs{r} \times \bs{v})\)が保存するため、
\begin{equation}
\frac{d}{d t}(\bs{r} \times \bs{v})=0
\end{equation}
が成り立つ。(角運動量保存については万有引力と保存則を参照)
これを\(\bs{l}=\bs{r} \times \bs{v}\)と置く。
あとはベクトルのノルムの微分公式 (証明はこちらから) \begin{equation} \frac{d}{dt} |\bs{x}(t)|=\frac{\bs{x} \cdot \dot{\bs{x}}}{|\bs{x}|} \end{equation} (ただし、\(\dot{\bs{x}}=\frac{d \bs{x}}{dt}\)である) を使うと、 \begin{eqnarray} \frac{d V_{s}}{dt}&=&\frac{1}{2}\frac{d}{dt}|\bs{l}| \nonumber \\ &=&\frac{\bs{l} \cdot \dot{\bs{l}}}{|\bs{l}|} \nonumber \\ &=&0 \quad (\because \dot{\bs{l}}=0) \end{eqnarray} となって、以上より \begin{equation} \frac{d V_{s}}{dt}=0 \tag{\ref{conservation}} \end{equation} を得る。