固有値と固有状態
演算子\(\hat{A}\)と波動関数\(\psi(x,t)\)に対し、以下が成り立つとする。(ただし、\(a\)は\(x,t\)によらない定数)
\begin{equation}
\hat{A} \psi(x,t) = a \ \psi(x,t)
\end{equation}
このとき、\(a\)を演算子\(\hat{A}\)の固有値、\(\psi(x,t)\)を演算子\(\hat{A}\)の固有状態(または固有関数)と呼ぶ。
固有値と固有状態は必ずセットで考える。
ある決められた演算を表す記号を演算子と呼びます(前回の記事参照)。 波動関数の中には、特定の演算子\(\hat{A}\)がかかった場合に、定数\(a\)倍されるものが存在し、 これを演算子\(\hat{A}\)の固有状態と呼びます。また、定数\(a\)を固有値と呼びます。ここでは具体例を通して固有状態 と固有値の物理的な意味を解説します。
具体例(レベル2)
具体例を眺めてイメージを養いましょう。
具体例その1(位置の固有状態)
位置演算子\(\hat{x} = x\)について、\(\psi_{a}(x) = \delta(x-a)\)とおくと、 デルタ関数の公式より \begin{equation} \hat{x} \psi_{a}(x) = a \ \psi_{a}(x) \end{equation} が成り立つ。 よって、状態\(\psi_{a}(x) = \delta(x-a)\)は、位置演算子\(\hat{x}\)の、固有値\(a\) に属する固有状態。
同様に、\(\psi_{b}(x) = \delta(x-b)\)について \begin{equation} \hat{x} \psi_{b}(x) = b \ \psi_{b}(x) \end{equation} が成り立つ。 よって、状態\(\psi_{b}(x) = \delta(x-b)\)は、位置演算子\(\hat{x}\)の、固有値\(b\) に属する固有状態。
このように、一つの演算子\(\hat{x} = x\)に対し、一般には複数の異なる 固有状態が存在する。また、固有状態は固有値とペアで存在するため、(一部の例外を除き) 異なる固有状態の数だけ異なる固有値が存在する。
位置演算子の固有状態はデルタ関数\(\psi_{a}(x) = \delta(x-a)\)です。固有値\(a\)は、デルタ関数のピークの 座標値そのものです。普通、「位置演算子の固有状態」は長いので略して「位置の固有状態」と呼びます。
具体例その2(運動量の固有状態)
運動量演算子\(\hat{p} = -i\hbar \pdiff{}{x}\)に対し、\(\psi_{k}(x) = N e^{i kx}\)(\(N,k\)は定数)とおくと、
\begin{equation}
\hat{p} \psi_{k}(x) = -i\hbar \pdiff{}{x} N e^{i kx} =\hbar k \ \psi_{k}(x)
\end{equation}
が成り立つ。
よって、\(\psi_{k}(x) = N e^{i kx}\)は、運動量演算子\(\hat{p}\)の、固有値\(\hbar k\)
に属する固有状態。
運動量演算子の固有状態は平面波\(\psi_{k}(x) = N e^{i kx}\)です。固有値\(\hbar k\)は平面波の運動量そのものです。
具体例その3(エネルギーの固有状態)
\(V(x)=0\)の系において、ハミルトニアンは\(\hat{H} = -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} \)であるが、
\(\psi_{K}(x) = N e^{i Kx} + M e^{-iKx}\)(\(N,M,K\)は定数)とおくと、
\begin{eqnarray}
\hat{H} \psi_{K}(x) &=& -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} \left( e^{i Kx}+ M e^{-iKx} \right) \nonumber \\
&=& \frac{\hbar^2 K^2}{2m} \psi_{K}(x)
\end{eqnarray}
を満たす。
よって、\(\psi_{K}(x) = N e^{i Kx}+ M e^{-iKx}\)は、ハミルトニアン\(\hat{H}= -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} \)の、固有値\(\frac{\hbar^2 k^2}{2m} \)
に属する固有状態。
ハミルトニアン\(\hat{H}= -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} \) の固有状態は、平面波の重ね合わせ\(\psi_{K}(x) = N e^{i Kx} + M e^{-iKx}\)です。固有値\(\frac{\hbar^2 k^2}{2m} \)は状態のエネルギーそのものです。
また、前述の運動量の固有状態\(\psi_{k}(x) = N e^{i kx}\)は、 同時にハミルトニアン\(\hat{H}= -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} \)の固有状態にも なっています。実際、以下が成り立ちます。 \begin{eqnarray} \hat{H} \psi_{k}(x) &=& -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} N e^{i kx} \nonumber \\ &=& \frac{\hbar^2 k^2}{2m} \psi_{k}(x) \end{eqnarray} このように、複数の異なる演算子に対し、同時に固有状態になる状態 がたまに存在し、これを同時固有状態と呼びます。 今回の例で言うと、\(\psi_{k}(x) = N e^{i kx}\)は運動量演算子\(\hat{p}\)とハミルトニアン\(\hat{H}\)の同時固有状態です。
固有状態ではない例
位置演算子\(\hat{x} = x\)を運動量の固有状態\(\psi_{k}(x) = N e^{i kx}\)に作用させると、 \begin{equation} \hat{x} \psi_{k}(x) = N x e^{i kx} \end{equation} のように、定数倍されることなく、寧ろ別の状態に変化する。 実際、右辺の状態を\(\bar{\psi}_{k}(x) = N x e^{i kx}\)と置くと \begin{eqnarray} \hat{p} \bar{\psi}_{k}(x) &=& -i\hbar \pdiff{}{x} N x e^{i kx} &=& (\hbar k+\frac{1}{x}) \ N x e^{i kx} &\neq& \hbar k \bar{\psi}_{k}(x) \end{eqnarray} であって、\(\bar{\psi}_{k}(x)=\hat{x} \psi_{k}(x)\)は運動量の固有状態ではなくなっている(元の状態とは別の状態に変化した)。
固有状態ではない状態とは、演算子が作用されることで関数の形(\(x\)の依存性)が変わってしまう 波動関数のことです。例えば\(\psi_{k}(x) = N e^{i kx}\)は、 \(\hat{x}=x\)がかかることで\(x\)の関数として別物に変化してしまうため、固有状態にはなりません。
物理的な意味(レベル2)
位置演算子\(\hat{x}\)に対し、 \begin{equation} \label{xev} \hat{x} \psi(x,t) = a \ \psi(x,t) \end{equation} を満たす固有状態\(\psi(x,t) = \delta(x-a)\)は、位置の測定値がばらつきなく\(a\)に 決まる状態を表す。
位置の固有状態の物理的な意味です。 デルタ関数が下の図のように、ある一点でのみ値を持つ関数であることを思い出すと (下の図では\(\delta(x)\)を図示しています。)、波動関数の物理的解釈から、\(\psi(x,t) = \delta(x-a)\) とは、\(x=a\)でしか粒子が発見されない状態を表していることになります。(波動関数の物理的意味についてはこちらから)
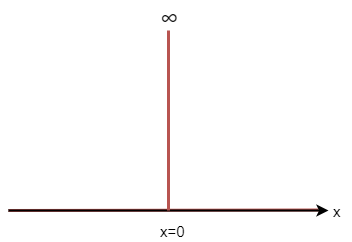
一般には、量子揺らぎがあるため、量子状態の位置を測定しても、その値は一意に決まりません。 しかし、位置の固有状態は特別(例外)で必ず\(x=a\)で粒子が観測されます。
これを踏まえると、(\ref{xev})式は、状態\( \psi(x,t)\)の位置\(x\)を観測した結果、 \(a\)という観測値を得た、という意味に解釈できます。つまり、位置演算子\(\hat{x}\)は位置の観測を表し、 右辺の固有値\(a\)はその観測値を表すというわけです。
ほかの例として、運動量の固有状態\(\psi(x,t) = N e^{i kx}\)を考えてみましょう。 \(\psi(x,t)\)をフーリエ変換したものを\(\tilde{\psi}(k,t)\)と置くと、 \begin{equation} \tilde{\psi}(k,t) = \delta(\frac{p}{\hbar}- k) \end{equation} であり、波数(運動量)空間上ではデルタ関数になります。これは運動量が\(p=\hbar k\)に一意に決まることを意味します。
このように、一般に演算子\(\hat{A}\)固有状態は、その\(\hat{A}\)に対応する観測可能量(物理量)の 測定値についてばらつきがなく、固有状態に対応する固有値\(a\)に一意に決まる状態を意味するわけです。
観測可能量\(A\)に対応する演算子\(\hat{A}\)に対し、 \begin{equation} \hat{A} \psi(x,t) = a \ \psi(x,t) \end{equation} を満たす固有状態\(\psi(x,t)\)は、\(A\)の測定値がばらつきなく\(a\)に 決まる状態を表す。
固有値と期待値の違い(レベル2)
一回毎の測定で得られる値を測定値と呼び、無限に繰り返し測定したときの 測定値の平均を期待値と呼ぶ。一方、何度測定しても同じ測定値しか得られなかった場合、 その測定値を固有値と呼ぶ。
測定値、期待値、固有値の説明です。具体例を見てイメージを掴みましょう。
具体例:位置の固有状態
状態\(\psi(x,t)\)の位置を測定したとき、毎測定ごとに得られる位置の値は測定値です。 無限に位置の測定を繰り返したとき、測定した位置の平均値が期待値です。
仮に、状態\(\phi(x,t)\)の位置の測定を繰り返した結果、常に原点(\(x=0\))に粒子の位置が観測されたとします。 このとき、\(x=0\)を位置の固有値と呼びます。また、\(\phi(x,t)\)を固有値\(x=0\)に対応する固有状態と呼びます。 繰り返しますが、固有値と固有状態は必ずセットで考えます。