アンペールの法則
静磁場\(\bs{B}(\bs{r})\)と定常電流の電流密度\(\bs{j}(\bs{r})\)の間には \begin{equation} \label{diffform} \nabla \times \bs{B}(\bs{r})= \mu_{0} \bs{j}(\bs{r}) \end{equation} が成り立つ。これを微分型(微分形)のアンペールの法則と呼ぶ。 (ただし\(\mu_{0}\)は真空の透磁率)
アンペールの法則はマクスウェル方程式の紹介に出てきた、 「アンペール・マクスウェルの法則」 \begin{eqnarray} & \ & \nabla \times \bs{B}(\bs{r},t) \nonumber \\ & \ & = \mu_{0} \bs{j}(\bs{r},t)+\varepsilon _{0}\mu_{0} \pdiff{\bs{E}}{t}(\bs{r},t) \end{eqnarray} の後ろの項が落ちた特殊な場合です。具体的には、電場と磁場が時間に依存しない場合 \(\pdiff{\bs{E}}{t}=\pdiff{\bs{B}}{t}=0\)の場合がこれに相当します。
また、式中の\(\nabla \times \bs{B}(\bs{r})\)は\(\bs{B}(\bs{r})\)の回転です。 (回転について未習の人はベクトルの回転からどうぞ) この法則について簡単にまとめました。
積分形(レベル1)
静磁場\(\bs{B}(\bs{r})\)と電流\(I\)の間には \begin{equation} \label{intform} \oint_{C} \bs{B}(\bs{r}) \cdot d \bs{r} = \mu_{0} I \end{equation} が成り立つ。これを積分型(積分形)のアンペールの法則と呼ぶ。 (ただし\(\mu_{0}\)は真空の透磁率)
冒頭で紹介したのは微分形でしたが、アンペールの法則には積分形もあります。 見た目は違いますが、両者は同じ意味です。(導出など詳しくは下のギモン参照。)
基本的に計算ではこちらの積分形を使います。微分形の意義や必要性に ついてはこちらの記事を参照。
法則の意味(レベル1)
アンペールの法則(\ref{intform})式の意味は、右ねじの法則の定量的な形。
まずは、アンペールの法則の意味について簡単に説明します。高校物理でも右ねじの法則と あるように、電流を流すと、その向きに対応して図1のように磁場が周囲に作られます。
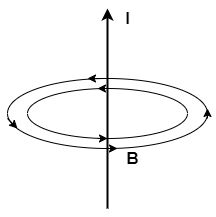
アンペールの法則では、電流によって作られる磁場\(\bs{B}\)を周回積分( 電流の周囲を一周する経路での積分)との間に、(\ref{intform})式の関係があることを述べています。 つまり、電流\(I\)が大きくなるほど、磁場も強くなるというわけです。
右ねじの法則との違いは、磁場\(\bs{B}\)の強さを電流\(I\)によって数式として表していることですね。
法則の導出(レベル1)
ここでは高校物理の内容から出発してアンペールの法則を導きます。まず、
導出が簡単な積分形(\ref{intform})式を先に導いた後、ストークスの定理から
微分形(\ref{diffform})式を導きます。
ストークスの定理について詳しくはこちらから。
導出
まず、高校物理で電流\(I\)が距離\(a\)の地点に作る 磁場\(H=|\bs{H}|\)が \begin{equation} H=\frac{I}{2 \pi a} \end{equation} で書けることを学んだと思いますが、これを変形していきます。
最初に、関係式 \begin{equation} B=\frac{1}{\mu_{0}} H \end{equation} を使って\(H\)を\(B=|\bs{B}|\)に書き換える。
\begin{equation} 2 \pi a B=\mu_{0} I \end{equation}ここで、左辺について
\begin{equation}
2 \pi a B= \oint_{r=aの円周} \bs{B}(\bs{r}) \cdot d \bs{r}
\end{equation}
のように周回積分に書き換えることができる。
なぜなら、電流から距離\(a\)の円周上に作られる磁場
は実験事実から一定であって、これにより
\begin{eqnarray}
& \ & \oint_{r=aの円周} \bs{B}(\bs{r}) \cdot d \bs{r} \nonumber \\
&=& |\bs{B}| \oint_{r=aの円周} r d \theta \nonumber \\
&=& 2 \pi a B
\end{eqnarray}
が得れられるからである。
途中、磁場が\(\theta\)方向であること(\(\bs{B}=|\bs{B}| \bs{e}_{\theta}\))
を使い、\(\bs{B}(\bs{r}) \cdot d \bs{r}=|\bs{B}| r d \theta\)と変形した。
(この積分について詳しくは→線積分、周回積分を参照。
今回は媒介変数を\(\theta\)として計算しています。)
以上より、まずは \begin{equation} \label{circleform} \oint_{r=aの円周} \bs{B}(\bs{r}) \cdot d \bs{r} =\mu_{0} I \end{equation} が言えた。つづいて、\(r=a\)の円周ではなく、一般の周回する経路\(C\)について 同じ関係が成り立つことを示せれば \begin{equation} \oint_{C} \bs{B}(\bs{r}) \cdot d \bs{r} = \mu_{0} I \tag{\ref{intform}} \end{equation} が示せたことになる。そのために、半径の異なる微小な円弧をつなげ合わせ、 \(C\)を再現することを試みる。 (似たような議論は既にガウスの法則でもやっている。)
今(\ref{circleform})式について、右辺は積分する円周の半径\(a\)に依存しない。 つまり、一周さえしていれば、どのように断片をつなげても電流を囲っている限り右辺は変わらないので \begin{eqnarray} & \ & \sum_{a} \sum_{l(a)} \oint_{r=aの円周の断片l(a)} \bs{B} \cdot d \bs{r} \nonumber \\ & \ & = \mu_{0} I \end{eqnarray} が成り立つはずである。そして、断片の区切りを短くし、近似の精度を限りなく上げていく。 すると、左辺の積分は経路\(C\)の積分に一致する。ゆえに、 \begin{equation} \oint_{C} \bs{B}(\bs{r}) \cdot d \bs{r} = \mu_{0} I \tag{\ref{intform}} \end{equation} が言えた。
最後に、(\ref{intform})式から、(\ref{diffform})式を導く。これはまず左辺にストークスの定理 を使えば \begin{equation} \oint_{C} \bs{B}(\bs{r}) \cdot d \bs{r}=\int_{S} \bs{B}(\bs{r}) \cdot \bs{n}(\bs{r}) dS \end{equation} と変形でき、(ストークスの定理について詳しくは→ストークスの定理参照) 右辺について、電流密度の定義から \begin{equation} I=\int_{S} \bs{j}(\bs{r}) \cdot \bs{n}(\bs{r}) \mathrm dS \end{equation} が成り立つ。(電流密度について詳しくは→電流密度からどうぞ)
この二つの式を(\ref{intform})式に適用すると \begin{eqnarray} & \ & \int_{S} \nabla \times \bs{B}(\bs{r}) \cdot \bs{n}(\bs{r}) \mathrm dS \nonumber \\ & \ & = \mu_{0} \int_{S} \bs{j}(\bs{r}) \cdot \bs{n}(\bs{r}) \mathrm dS \end{eqnarray} を得るが、両辺を比較して \begin{equation} \nabla \times \bs{B}(\bs{r})= \mu_{0} \bs{j}(\bs{r}) \tag{\ref{diffform}} \end{equation} が導出できた。